kd树的搜索过程到底是怎么进行的？

1 引言

KNN虽然理解起来很简单，但相比之下kd 树的最邻近和K邻近搜索过程还是略显复杂。在前面的文章中笔者已经对KNN的原理与sklearn使用示例进行了详细的介绍。不过到目前为止，还有一个问题没有解决的就是如何快速的找到当前样本点周围最近的K个样本点。通常来说，这一问题可以通过$kd$树来解决，下面开始介绍其具体原理。

2 $kd$树

2.1 $kd$树构造

$kd$树（$k$-dimensional tree）是一种空间划分数据结构，用于组织$k$维空间中的点，其本质上也就等同于二叉搜索树。不同的是，在$kd$树中每个节点存储的并不是一个值，而是一个$k$维的样本点[1]。在二叉搜索树中，任意节点中的值都大于其左子树中的所有值，小于或等于其右子树中的所有值，如图1所示。

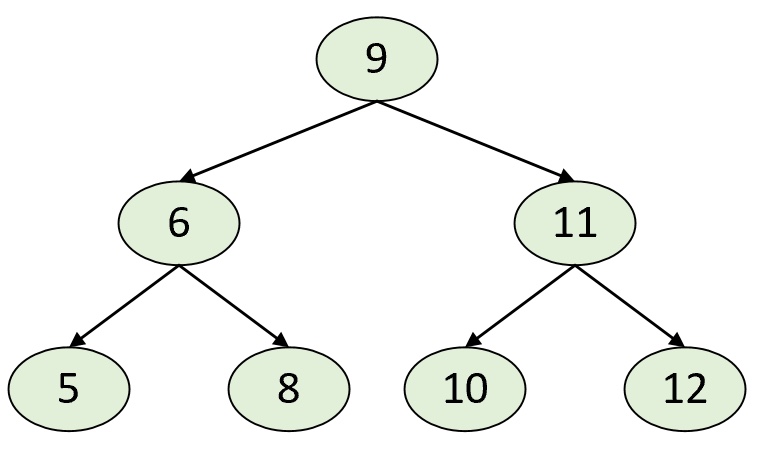
在$kd$树中，所有的节点也都满足类似二叉搜索树的特性，即左子树中所有的样本点均“小于”其父节点中的样本点，而右子树中所有的样本点均“大于”或“等于”其父节点中的样本点。因此可以看出，构造$kd$树的关键就在于如何定义任意两个$k$维样本点之间的大小关系。具体的，在构造$kd$树时，每一层的节点在划分左右子树时只会循环的选择$k$维中的其中一个维度进行比较。例如样本点中一共有$x,y$两个维度，那么在对根节点进行划分时可以以维度$x$对左右子树进行划分；接着再以维度$y$对根节点的孩子进行左右子树划分；进一步，根节点的孩子的孩子再以维度$x$进行左右子树划分，以此循环[2]。同时，为了使得最后得到的是一棵平衡的$kd$树，每次会选择当前子树中对应维度的中位数作为切分点。

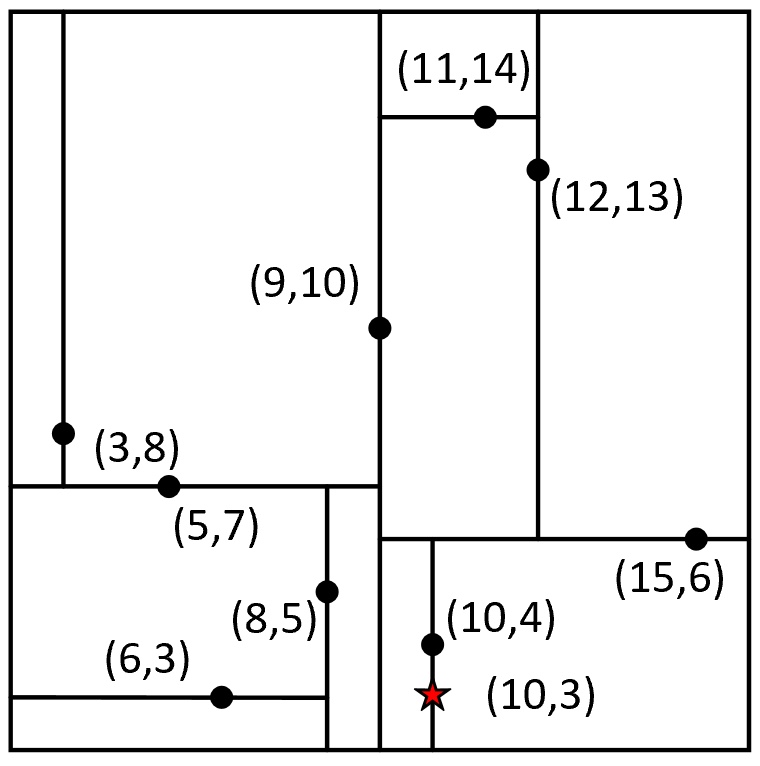
例如现在有样本点[5,7], [3,8], [6,2], [8,5], [15,6], [10,4], [12,13], [9,10],[11,14]，那么根据上述规则便可以构造得到如图2所示的$kd$树。

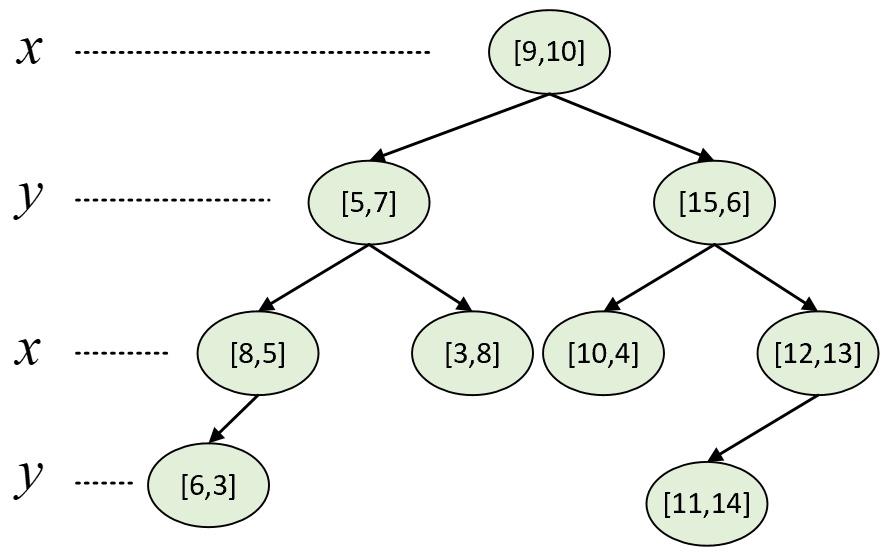
从图2可以看出，对于根节点来说，其左子树中所有样本点的$x$维度均小于9，其右子树的$x$维度均大于等于9；对于根节点的左孩子来说，其左子树中所有样本点的$y$维度均小于7，其右子树中所有样本点的$y$维度均大于等于7。当然，对于其它节点也都满足类似的特性。同时，根据$kd$树交替选择特征维度对样本空间进行划分的特性，以图2中的划分方式还能得到如图3所示的特征空间。

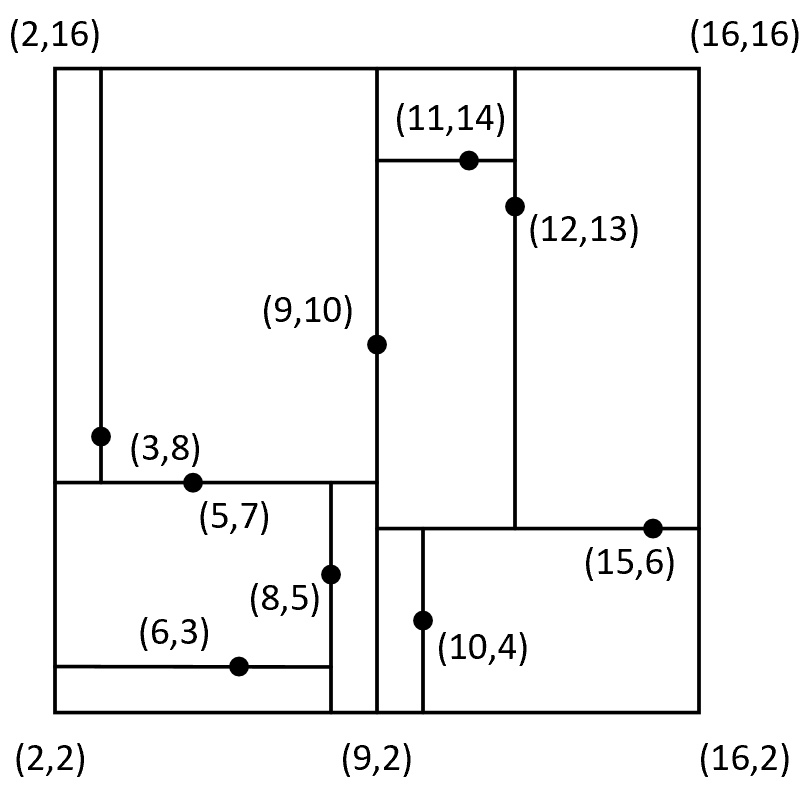
从图3中可以看出，整个二维平面首先被样本点[9,10]划分成了左右两个部分（对应图2中的左右子树），接着左右两个部分又各自分别被[5,7]和[15,6]划分成了上下两个部分，直到划分结束。到此，对于$kd$树的构造就介绍完了，接下来看如何通过$kd$树来完成搜索任务。

2.2 最近邻$kd$树搜索

在正式介绍K近邻（即最近的K个样本点）搜索前，笔者先来介绍如何利用$kd$树进行最近邻搜索。总的来说，在已知$kd$树中搜索离给定样本点$q$最近的样本点时，首先设定一个当前全局最佳点和一个当前全局最短距离，分别用来保存当前离$q$最近的样本点以及对应的距离；然后从根节点开始以类似生成$kd$树的规则来递归的遍历$kd$树中的节点，如果当前节点离$q$的距离小于全局最短距离，那么更新全局最佳点和全局最短距离；如果被搜索点到当前节点划分维度的距离小于全局最短距离，那么再递归遍历当前节点另外的一个子树，直至整个递归过程结束。具体步骤可以总结为[2]：

• (1) 设定一个当前全局最佳点和全局最短距离，分别用来保存当前离搜索点最近的样本点和最短距离，初始值分别为空和无穷大；
• (2) 从根节点开始，并设其为当前节点；
• (3) 如果当前节点为空，则结束；
• (4) 如果当前节点到被搜索点的距离小于当前全局最短距离，则更新全局最佳点和最短距离；
• (5) 如果被搜索点的划分维度小于当前节点的划分维度，则设当前节点的左孩子为新的当前节点并执行步骤(3)(4)(5)(6)；反之设当前节点的右孩子为新的当前节点并执行步骤(3)(4)(5)(6)；
• (6) 如果被搜索点到当前节点划分维度的距离小于全局最短距离，则说明全局最佳点可能存在于当前节点的另外一个子树中，所以设当前节点的另外一个孩子为当前节点并执行步骤(3)(4)(5)(6)；

递归完成后，此时的全局最佳点就是在$kd$树中离被搜索点最近的样本点。

这里需要明白一点的是，利用步骤(6)中的规则来判断另外一个子树中是否可能存在全局最佳点的原理如图4所示。

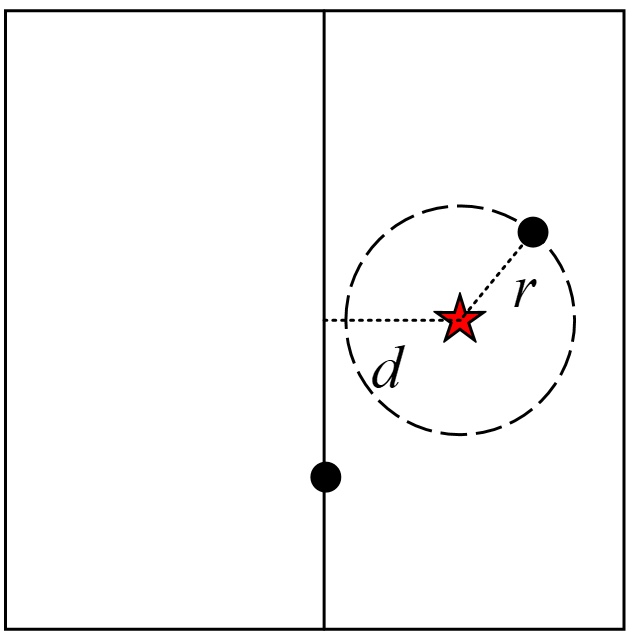
在图4中，右上角为当前全局最佳点，五角星为被搜索点。可以看到，此时的整个空间被下方的样本点划分成了左右两个部分（子树）。并且，五角星离左子树中样本点的最短距离为五角星到当前划分维度的距离$d$。显然，如果被搜索点到当前全局最佳点的距离$r$小于距离$d$，那么此时左子树中就不可能存在更优的全局最佳点。

当然，上述步骤还可以通过一个更清晰的伪函数来进行表达：

1
bestNode, bestDist = None, inf
2
def NearestNodeSearch(curr_node):
3
    if curr_node == None:
4
        return
5
    if distance(curr_node, bestNode) <bestDist:
6
        bestDist = distance(curr_node, bestNode)
7
        bestNode = curr_node
8
    if q_i < curr_node_i:
9
        NearestNodeSearch(curr_node.left)
10
    else:
11
        NearestNodeSearch(curr_node.right)
12
    if |curr_node_i - q_i| < bestDist:
13
        NearestNodeSearch(curr_node.other)

在上述代码中，q_i和curr_node_i分别表示被搜索点和当前节点的划分维度；curr_node.other表示curr_node.left和curr_node.right中先前未被访问过的子树。

2.3 最近邻搜索示例

在介绍完最近邻的搜索原理后再来看几个实际的搜索示例，以便对搜索过程有更加清晰的理解。如图5所示，左右两边分别是5.3.1节中所得到的$kd$树和特征划分空间，同时右图中的五角星为给定的被搜索点$q$，接下来开始在左边的$kd$树中搜索离$q$点最近的样本点。

在搜索伊始，全局最佳点和全局最短距离分别为空和无穷大。第1次递归：此时设根节点[9,10]为当前节点，因满足步骤(4)当前节点到被搜索点的距离小于当前全局最短距离，所以更新当前最佳点为[9,10]，全局最短距离为7.07。接着，由于被搜索点的划分维度10大于当前节点的划分维度9，因此设当前节点的右孩子[15,6]为新的当前节点。第2次递归：继续执行步骤(4)，由于此时当前节点到被搜索点的距离为5.83，小于全局最短距离，所以更新当前最佳点为[15,6]，全局最短距离为5.83。进一步，由于被搜索点的划分维度3小于当前节点的划分维度6，因此设当前节点的左孩子[10,4]为新的当前节点。第3次递归：继续执行步骤(4)，由于此时当前节点到被搜索点的距离为1，小于全局最短距离，所以更新当前最佳点为[10,4]，全局最短距离为1。此时，由于被搜索点的划分维度10大于等于当前节点的划分维度10，因此设当前节点的右孩子为新的当前节点，并进入第4次递归。

第4次递归：由于此时当前节点为空，所以第4次递归结束返回第3次递归，即此时的当前节点为[10,4]，并继续执行步骤(6)。由于被搜索点[10,3]到当前划分维度$x=10$的距离为0，小于全局最短距离1，说明全局最佳点可能存在于当前节点的左子树中（此时可以想象假如$kd$树中存在点[9.9,3]）,所以设当前节点的左孩子为新的当前节点。第5次递归：由于当前节点为空，所以第5次递归结束回到第3次递归中。返回第3次递归后，此时的当前节点为[10,4]，且已执行完步骤(6)，返回到第2次递归中。返回第2次递归后，此时的当前节点为[15,6]，并继续执行步骤(6)。由于被搜索点[10,3]到当前划分维度$y=6$的距离为3，大于全局最短距离，则说明节点[15,6]的右子树中不可能存在全局最佳点，此时返回到第1次递归中。返回第1次递归后，此时的当前节点为根节点[9,10]，并继续执行步骤(6)。由于被搜索点[10,3]到当前划分维度$x=9$的距离为1，大于等于全局最短距离1，所以当前节点的左子树中不可能存在全局最佳点。到此步骤(6)执行结束，即所有的递归过程都执行完毕。此时的全局最佳点中保存的点[10,4]便是$kd$树中离被搜索点[10,3]最近的样本点。

经过上述步骤后，相信读者朋友们对于$kd$树的搜索过程已经有了清晰的认识。同时，各位读者也可以自己来试着从上述$kd$树中来搜索离[8.9,4]最近的样本点。在搜索过程中会发现，一开始会从根节点进入左子树，并找到[8,5]为当前全局最佳点。但是当一步步回溯后会发现，原来右子树中的[10,4]才是真正离[8.9,4]最近的样本点。

2.4 K近邻$kd$树搜索

在介绍完最近邻的$kd$树搜索原理后便可以轻松的理解K近邻的$kd$树搜索过程。需要注意的是，这里的两个“K”分别表示两种不同的含义，前者表示要搜索得到离给定点最近的K个样本点，而后者表示的是样本点的维度。

总的来说K最近邻的搜索过程和最近邻的搜索过程类似，只是需要额外的维护一个大小为K的有序列表。在整个列表中，当前距离被搜索点最近的样本点放在首位，而距离被搜索点最远的样本点放在末尾。具体的搜索过程可以总结为：

• (1) 设定大小为K的有序列表用来保存当前离搜索点最近的K个样本点；
• (2) 从根节点开始，并设其为当前节点；
• (3) 如果当前节点为空，则结束；
• (4) 如果列表不满，则直接将当前样本插入到列表中；如果列表已满，则判断当前样本到被搜索点的距离是否小于列表最后一个元素到被搜索点的距离，成立则将列表中最后一个元素删除，并插入当前样本；（每次插入后仍有序）
• (5) 如果被搜索点的划分维度小于当前节点的划分维度，则设当前节点的左孩子为新的当前节点并执行步骤(3)(4)(5)(6)；反之设当前节点的右孩子为新的当前节点并执行步骤(3)(4)(5)(6)；
• (6) 如果列表不满，或者如果被搜索点到当前节点划分维度的距离小于列表中最后一个元素到被搜索点的距离，则设当前节点的另外一个孩子为当前节点并执行步骤(3)(4)(5)(6)；

递归完成后，此时离被搜索点最近的K个样本点就是有序列表中的K个元素。

上述步骤同样可以通过一个更清晰的伪函数来进行表达：

xxxxxxxxxx
16
1
KNearestNodes, n = [], 0
2
def NearestNodeSearch(curr_node):
3
    if curr_node == None:
4
        return
5
    if n < K:
6
        KNearestNodes.insert(curr_node)  # 插入后保持有序
7
    if n >= K and
8
        distance(curr_node, q) < distance(curr_node, KNearestNodes[-1]):
9
        KNearestNodes.pop()
10
        KNearestNodes.insert(curr_node)  # 插入后保持有序
11
    if q_i < curr_node_i:
12
        NearestNodeSearch(curr_node.left)
13
    else:
14
        NearestNodeSearch(curr_node.right)
15
    if n < K or | curr_node_i - q_i | < distance(q, KNearestNodes[-1]):
16
        NearestNodeSearch(curr_node.other)

在上述代码中，KNearestNodes[-1]表示取有序列表中的最后一个元素；q_i和curr_node_i分别表示被搜索点和当前节点的划分维度；curr_node.other表示curr_node.left和curr_node.right中先前未被访问过的子树。

2.5 K近邻搜索示例

下面，以图2中的$kd$树为例，来搜索离[10,3]最近的3个样本点。

在搜索伊始，有序列表为空，K为3。第一次递归：此时设根节点[9,10]为当前节点，因满足步骤(4)中的列表为空的条件，所以直接将根节点加入列表中，即此时KNearestNodes=([9,10])。接着，由于被搜索点的划分维度10大于当前节点的划分维度9，因此设当前节点的右孩子[15,6]为新的当前节点。第2次递归：继续执行步骤(4)，由于此时列表未满，所以直接将当前节点插入列表中，即此时KNearestNodes=([15,6], [9,10])。进一步，由于被搜索点的划分维度3小于当前节点的划分维度6，因此设当前节点的左孩子[10,4]为新的当前节点。第3次递归：继续执行步骤(4)，由于此时列表未满，所以直接将当前节点插入列表中，且由于[10,4]当前离被搜索点最近，所以应该放在列表最前面，即此时KNearestNodes=([10,4], [15,6], [9,10])。进一步，由于被搜索点的划分维度10大于等于当前节点的划分维度10，所以设当前节点的右孩子为新的当前节点，并进入第4次递归。

第4次递归：由于此时当前节点为空，所以第4次递归结束并返回到第3次递归中，即此时的当前节点为[10,4]，并继续执行步骤(6)。此时列表已满，但由于被搜索点[10,3]到当前划分维度$x=10$的距离为0，小于被搜索点到有序列表中最后一个样本点距离，说明可能存在一个比有序列表中最后一个元素更佳的样本点。所以设当前节点的左孩子为新的当前节点。第5次递归：由于当前节点为空，所以第5次递归结束回到第3次递归中。返回到第3次递归后，此时的当前节点为[10,4]，且已执行完步骤(6)，返回到第2次递归中。返回到第2次递归后，此时的当前节点为[15,6]，并继续执行步骤(6)。此时列表已满，但由于被搜索点[10,3]到当前划分维度$y=6$的距离为3，小于被搜索点到[9,10]的距离7.07，说明在当前节点[15,6]的右子树中可能存在一个比[9,10]更佳的样本点。所以设[15,6]的右孩子[12,13]为新的当前节点。第6次递归：此时列表已满，且由于当前节点到被搜索点的距离10.19，大于被搜索点到[9,10]的距离，所以继续执行步骤(5)。由于被搜索点的划分维度10小于当前节点的划分维度12，所以设[11,14]为新的当前节点，并进入第7次递归。

第7次递归：此时列表已满，且由于当前节点到被搜索点的距离11.04，大于被搜索点到[9,10]的距离，所以继续执行步骤(5)。由于被搜索点的划分维度3小于当前节点的划分维度14，所以设[11,14]的左孩子为新的当前节点。第8次递归：由于此时当前节点为空，所以第8次递归结束并返回到第7次递归中，即此时的当前节点为[11,14]，并继续执行步骤(6)。此时列表已满，且由于被搜索点[10,3]到当前划分维度$y=14$的距离为11，大于被搜索点到有序列表中最后一个样本点距离，所以第7次递归结束并回到第6次递归。

返回第6次递归后，此时的当前节点为[12,13]，继续执行步骤(6)。此时列表已满，且由于被搜索点[10,3]到当前划分维度$x=12$的距离为2，小于被搜索点到有序列表中最后一个样本点的距离，说明当前节点[12,13]的右子树中存在比[9,10]更近的点（可以想象假设存在点[12.1,6.1]），所以设[12,13]的右孩子为新的当前节点。第9次递归：由于此时当前节点为空，所以第9次递归结束并返回到第6次递归中，即此时的当前节点为[12,13]，且已经执行完步骤(6)，进而返回到第2次递归。返回到第2次递归后，此时的当前节点为[15,6]，且已执行完步骤(6)，进而返回到第1次递归中。

返回第1次递归后，此时的当前节点为[9,10]，继续执行步骤(6)。此时列表已满，但由于被搜索点[10,3]到当前划分维度$x=9$的距离为1，小于被搜索点到有序列表中最后一个样本点的距离，说明当前节点[9,10]的左子树中存在比[9,10]更近的点（从图5-7中一眼便能看出，例如点[8,5]），所以设[5,7]为新的当前节点。第10次递归：此时列表已满，但由于当前节点到被搜索点的距离6.4，小于被搜索点到有序列表中最后一个样本点[9,10]的距离7.07，因此更新KNearestNodes=([10,4], [15,6], [5,7])，并继续执行步骤(5)。由于被搜索点的划分维度3小于当前节点的划分维度7，所以设[8,5]为新的当前节点，并进入第11次递归。

第11次递归：此时列表已满，但由于当前节点到被搜索点的距离2.83，小于被搜索点到有序列表中最后一个样本点[5,10]的距离6.4，因此更新KNearestNodes=([10,4], [8,5], [15,6])，并继续执行步骤(5)。由于被搜索点的划分维度10大于当前节点的划分维度8，所以设[8,5]的右孩子为新的当前节点。第12次递归：由于此时当前节点为空，所以第12次递归结束并返回到第11次递归中，即此时的当前节点为[8,5]，并继续执行步骤(6)。此时列表已满，但由于被搜索点[10,3]到当前划分维度$x=8$的距离为2，小于被搜索点到有序列表中最后一个样本点的距离，所以设[6,3]为新的当前节点，并进入第13次递归。

第13次递归：此时列表已满，但由于当前节点到被搜索点的距离4.0，小于被搜索点到有序列表中最后一个样本点[5,10]的距离5.83，因此更新KNearestNodes=([10,4], [8,5], [6,3])，并继续执行步骤(5)。由于被搜索点的划分维度3大于等于当前节点的划分维度3，所以设[6,3]的右孩子为新的当前节点。第14次递归：由于此时当前节点为空，所以第14次递归结束并返回到第13次递归中，即此时的当前节点为[6,3]，并继续执行步骤(6)。此时列表已满，但由于被搜索点[10,3]到当前划分维度$y=3$的距离为0，小于被搜索点到有序列表中最后一个样本点的距离，说明[6,3]的左子树中存在比[6,3]更近的点（可以想象假设存在点[7,2.9]），所以设[6,3]的左孩子为新的当前节点，并进入第15次递归。

第15次递归：由于此时当前节点为空，所以第15次递归结束并返回到第13次递归中，即此时的当前节点为[6,3]，且已经执行完步骤(6)进一步返回第11次递归中。返回第11次递归后，此时的当前节点为[8,5]，且已经执行完步骤(6)进一步返回第10次递归中。返回第10次递归后，当前节点为[5,7]，继续执行步骤(6)。由于此时列表已满，且被搜索点[10,3]到当前划分维度$y=7$的距离4，大于等于被搜索点到有序列表中最后一个样本点[6,3]的距离，所以[5,7]的右子树中不可能存在比[6,3]更近的点，故返回第1次递归。

在返回到第1次递归后，此时的当前节点为[9,10]，且已执行完步骤(6)，即所有的递归过程结束。此时有序列表中的元素便为$kd$树中离被搜索点[10,3]最近的3个样本点，即KNearestNodes=([10,4], [8,5], [6,3])。整个递归过程顺序如图6所示。

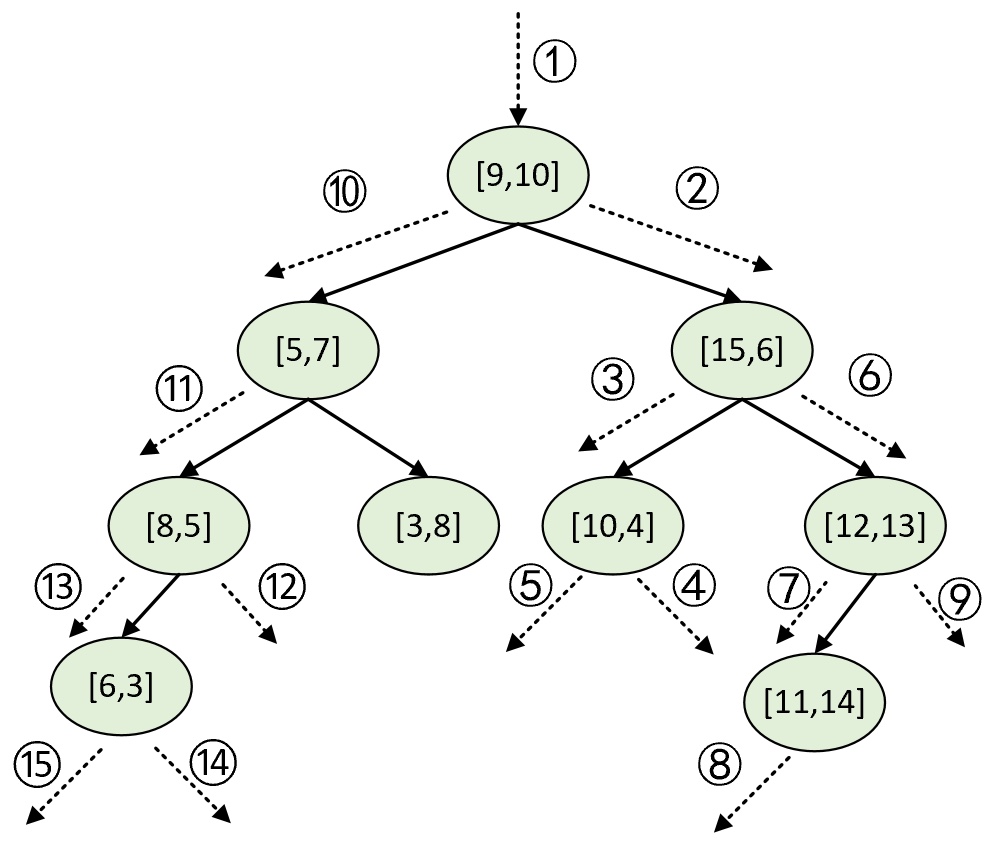
到此，对于K近邻算法的原理就介绍完了。

3 总结

在本节中，笔者首先介绍了$kd$树的基本原理，以及如何来构造一棵$kd$树；接着介绍了如何通过$kd$树来搜索离给定点最近的样本点，并通过一个实际的搜索示例来进行了详细的介绍；最后介绍了如何在最近邻的基础上，在$kd$树中来搜索离给定点最近的K个样本点，即K近邻搜索。

本次内容就到此结束，感谢您的阅读！如果你觉得上述内容对你有所帮助，欢迎分享至一位你的朋友！若有任何疑问与建议，请添加笔者微信'nulls8'或加群进行交流。青山不改，绿水长流，我们月来客栈见！

引用

[1] https://en.wikipedia.org/wiki/K-d_tree

[2] http://web.stanford.edu/class/cs106l/