1 引言2 精确率与召回率2.1 准确率弊端2.2 精确率与召回率原理2.3 准确率与召回率区别3 Precision-Recall 曲线3.1 Precision-Recall 曲线原理3.2 AUC计算4 代码实现4.1 指标计算4.2 结果可视化5 总结引用
1 引言
各位朋友大家好,欢迎来到月来客栈,我是掌柜空字符。
在之前的文章中虽然掌柜已经详细介绍过精确率(Precision)和召回率(Recall)的计算原理与实现,但是并没有介绍在有了准确率(Accuracy)之后为什么还需要精确率和召回率,以及精确率和召回率除了作为一种常见的评价指标来使用还有没有别的用途。在接下来的这篇文章中,掌柜将会首先介绍为什么需要精确率和召回率;然后再以另外一个视角来回顾精确率和召回率;最后再来介绍筛选模型的另外两个诊断工具ROC Curve和Precision-Recall Curve。
2 精确率与召回率
通常来说,之所以会出现新的评价指标很大程度上都是因为原有评价指标在某些特定情况下存在着严重的不足之处。在分类问题中,对于准确率这一评价指标来说,其不足之处就在于当我们面对的是一个正负样例严重不均衡的分类任务时如果仅采用准确率作为评价指标,那模型的预测结果将会严重误导我们的决策。
2.1 准确率弊端
例如现在需要训练一个癌细胞诊断模型,在训练数据中其中负样本(非癌细胞)有10万个,而正样本(癌细胞)只有200个。假如某个模型将其中的105个预测为正样本,100095个预测为负样本。最终经过核对后发现,正样本中有5个预测正确,负样本中有99900个样本预测正确。那么此时该模型在训练集上的准确率为:
但显然,这样的一个模型对于辅助医生决策来说并没有任何作用。因此,在面对类似这样样本不均衡的任务中,并不能够将准确率作为评价模型的唯一指标。此时就需要引入精确率和召回率来作为新的评价指标。
2.2 精确率与召回率原理
虽然在之前逻辑回归的讲解以及文章多分类任务下的召回率与F值中掌柜已经详细介绍了什么是精确率与召回率以及各自的计算方法,但是掌柜下面将会从另外一个视角来介绍精确率与召回率。
假定现在有一个猫狗识别程序,并且假定狗为正类别(Positives)猫为负类别(Negatives)。程序在对12张狗和10张猫的混合图片进行识别后,判定其中8张图片为狗,14张图片为猫。在这8张程序判定为狗的图片中仅仅只有5张图片的确为狗,因此这5张图片就被称为正确的正样本(True Positives, TP),而余下的3张被称为错误的正样本(False Positives, FP)。同时可以得出,此时12张狗中的7张狗被程序误判为了猫,而这7张就被称之为错误的负样本(False Negatives, FN);并且14张被判定为猫的图片中仅有7张为真实的猫,即正确的负样本(True Negatives, TN)。整个结果分布如图1所示[2]。

如图1所示,整个矩形左边部分为正样本(relevant elements),矩形右边部分为负样本;中间的圆形区域为识别到的正样本(retrieved elements);左边与圆相交的部分为TP,其余部分为FN;右边与圆相交部分为FP,其余部分为TN。
因此,该程序识别正样本狗的精确率为:
识别正样本狗的召回率率为:
同时,精确率和召回率的计算公式还可以通过图2来进行表示:

从图2可以看出,精确率衡量的是在所有检索出的样本(程序识别为“狗”)中有多少是真正所期望被检索(真实为狗)出的样本;召回率衡量的则是在所有被期望检索(真实为狗)出的样本中,到底检索出了多少样本。
在这里尤其需要注意的一点是,从图2可以看出在计算召回率时其分母(即
例如:某一次掌柜在使用搜索引擎搜索掌柜需要的内容时,搜索引擎一共返回了30个搜索页面,掌柜逐一阅读后发现其中只有20个页面与掌柜检索的内容相关。同时,掌柜开天眼后得知其实还存在另外50个与内容相关的页面搜索引擎并没有返回。那么此时该搜索引擎对于掌柜搜索内容结果的精确率就是
从上面的内容可知,精确率和召回率分别从不同的角度来衡量了一个模型的表现能力,其中精确率衡量的是模型发现正样本相关性的能力,而召回率则是衡量模型在整个数据集中发现正样本的能力,并且可以发现两者的结果都是越大越接近于1越好。
在清楚精确率和召回率的原理之后再来看2.1节中癌细胞的识别模型,则此时有:
- TP(表示将正样本预测为正样本,即预测正确)为:
- FN(表示将正样本预测为负样本,即预测错误)为:
- FP(表示将负样本预测为正样本,即预测错误)为:
- TN(表示将负样本预测为负样本,即预测正确)为:
那么
从计算结果可以发现,尽管这个癌细胞判别模型的准确率很高,但是从精确率和召回率来看则非常糟糕。
2.3 准确率与召回率区别
介绍到这里可能有朋友会问,在上述问题中既然精确率和召回率都能够解决准确率所带来的弊端,那可不可以只用其中一个呢?答案是不可以。
这里掌柜再次以上面的癌细胞判别程序为例,并以三种情况来进行示例说明:
情况一:将训练集中的所有样本均预测为正样本,此时有
情况二:将训练集其中的50个预测为正样本,100150个预测为负样本。最终经过核对后发现,正样本中有50个预测正确,负样本中有100000个样本预测正确。此时有
情况三:将训练集其中的210个预测为正样本,99990个预测为负样本。最终经过核对后发现,正样本中有190个预测正确,负样本中有99980个样本预测正确。此时有
根据三种情况下的表现结果可以知道,如果仅从单一指标来看无论是准确率、精确率还是召回率都不能全面地来评估一个模型。并且,至少应该选择精确率和召回率同时作为评价指标。
此时可以发现,精确率和召回率之间总体上(不是绝对)存在着某种相互制约的关系,即类似于此消彼长的情况。可能模型某些时候取得了较高的召回率但是精确率却很低,也可能是取得了较高的精确率但召回率却很低。所以,在实际情况中我们会根据需要来选择不同的侧重点,当然最理想的情况就是在取得高召回率的同时还能保持较高的精确率。
因此,我们还可以通过一个统一的指标来衡量模型的召回率与精确率,即
其中用到频率最高的是当
因此,上述三种情况对应的
所以,对于一个分类模型来说,如果想要在精确率和召回率之间取得一个较好的平衡,最大化
3 Precision-Recall 曲线
在机器学习的二分类问题中,以逻辑回归为例,模型首先输出的是当前样本属于正类别的概率值,然后再根据一个指定的阈值来判定其是否为正类,并且通常情况下该阈值默认为0.5。但是,我们依旧可以根据实际情况来调整这一阈值从而获得更好的模型预测结果。由此,便可以根据阈值的变化来计算得到不同阈值下的精确率和召回率并绘制成一条曲线,而这条曲线就被称为Precision-Recall Curve(PR Curve)。
通过PR曲线,我们便可以清楚地观测到精确率与召回率的变化情况,以此来选择一个合理的阈值。
3.1 Precision-Recall 曲线原理
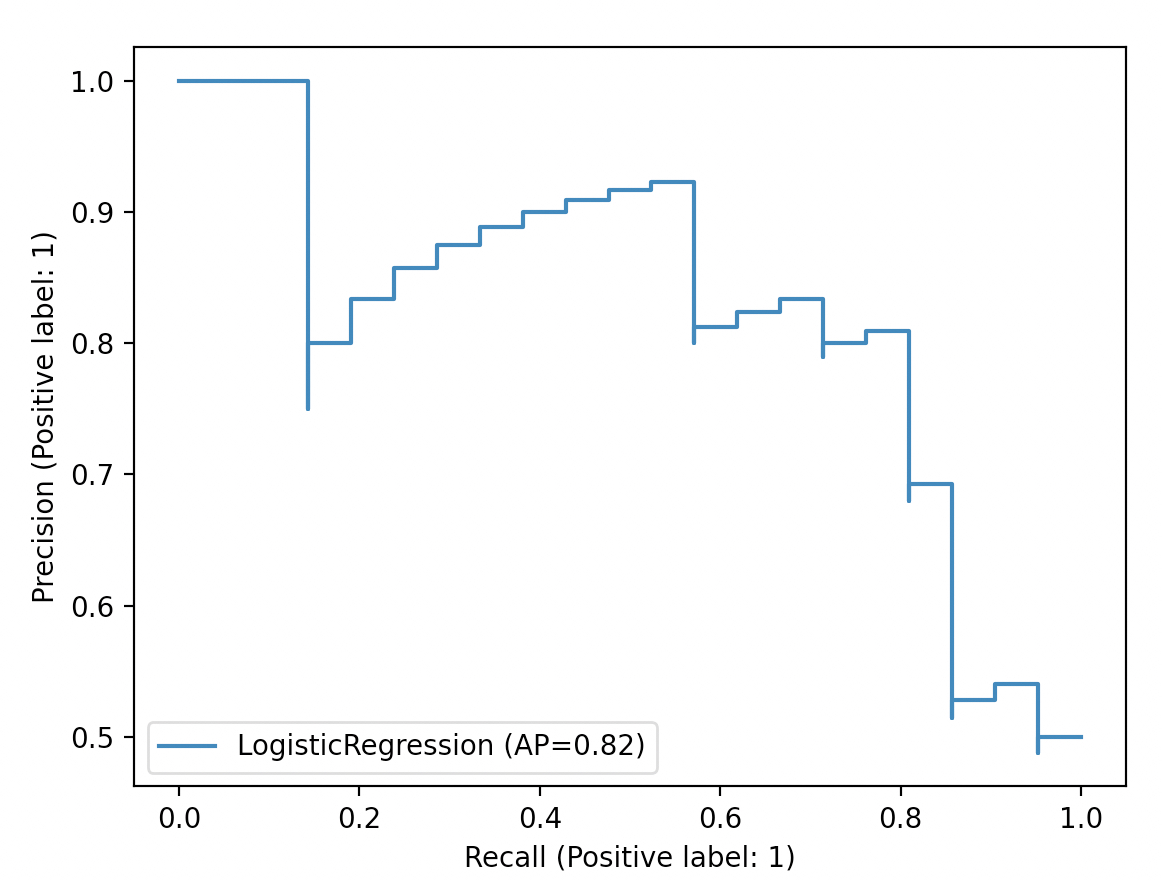
如图3所示,横纵坐标分别为不同阈值下的召回率Recall和精确率Precision,蓝色图像便是绘制得到的Precision-Recall曲线。
对于精确率来说,根据公式
对于召回率来说,根据公式
总结起来就是,随着召回率的增大,那么精确率整体上可能会呈下降趋势,如图3所示。因此,Precision-Recall曲线很好地展示了在不同阈值取值下精确率和召回率的平衡情况。同时,从上面的分析可知,最理想的情况便是随着召回率的提升,精确率也逐步保持提升或保持不变。
3.2 AUC计算
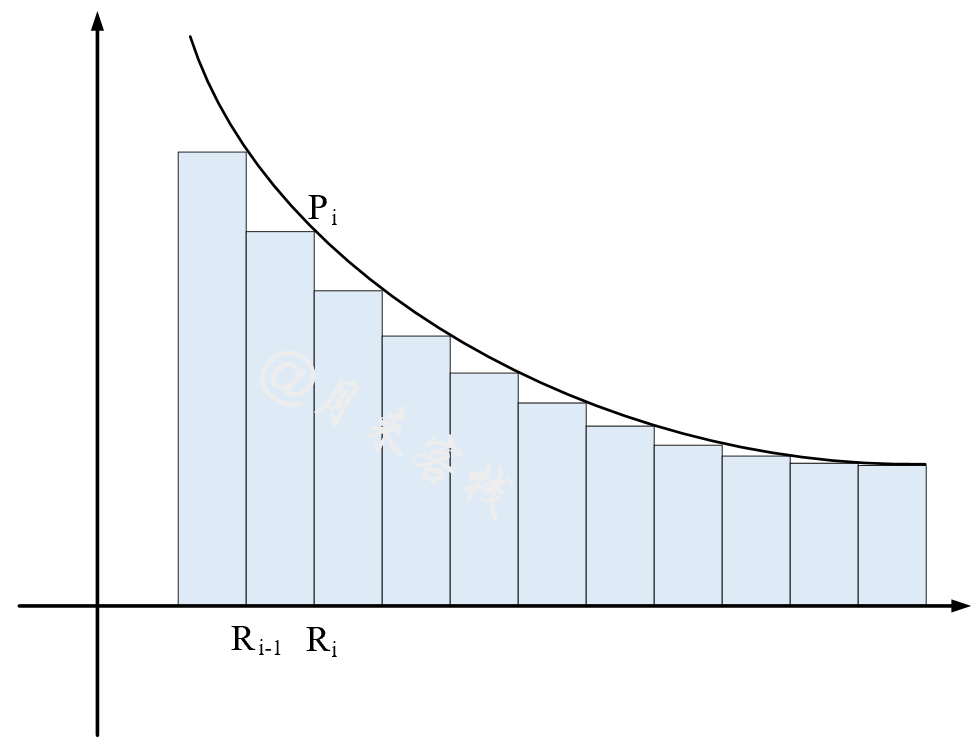
虽然通过PR曲线能够有效地观察模型在不同阈值下精确率和召回率的变化情况,但是在不同模型之间却很难进行比较。此时,在基于PR曲线的基础上,可以通过计算曲线下面积(Area Under the Curve, AUC)来得到一个整体的评估值,如图4所示。
如图4所示,PR曲线投影至
由于并不知道PR曲线对应的函数不能用积分进行求解,因此只能采用近似的方法来求得曲线与
对于矩形规则来说[5],其主要思想是将
计算公式为:
其中
从公式
对于梯形规则来说[8],其主要思想则是将
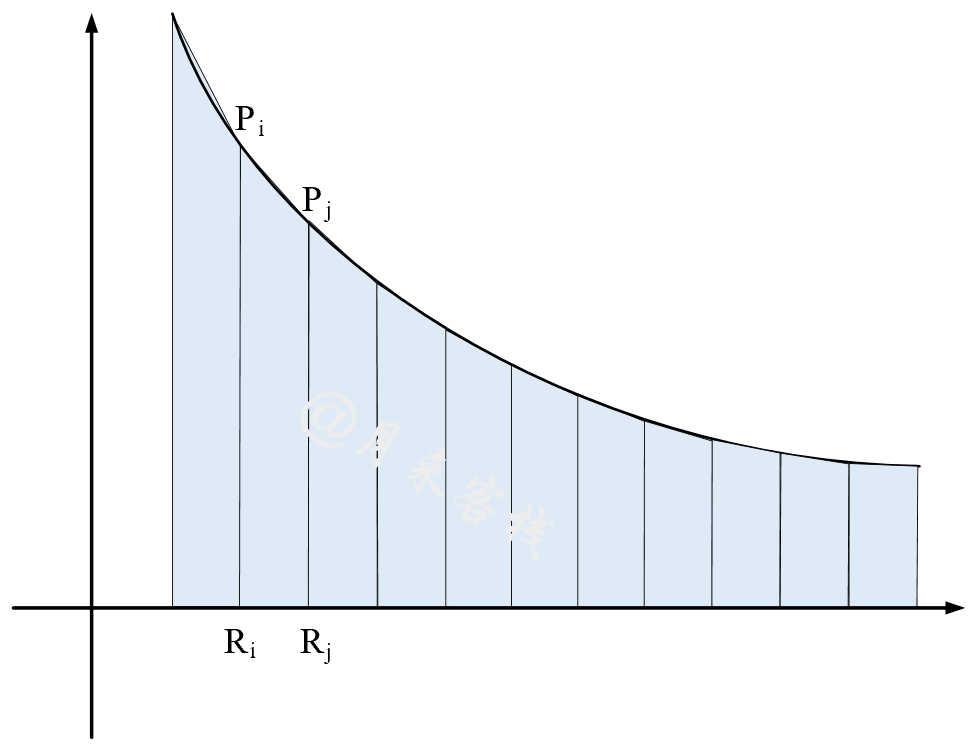
计算公式为:
其中
这里需要注意的是,由于上述两种计算AUC的方法采用了不同的策略,因此最终两者计算得到的结果并不相等。
4 代码实现
下面,掌柜将先来介绍如何通过编码实现不同阈值下召回率和精确率的计算、AUC计算和Precision-Recall曲线的可视化;然后再来介绍如何通过sklearn提供的接口来完成上述过程。以下所有示例代码均可从词仓库[11]中获取!
4.1 指标计算
首先我们需要定义一个预测函数,根据不同的阈值输出不同的预测结果,代码如下:
21def predict(y_scores, threholds):2 return (y_scores >= threholds) * 1接着再定义一个函数来计算精确率和召回率,代码如下:
51from sklearn.metrics import precision_score, recall_score2def compute_scores(y_true, y_pred):3 p_score = precision_score(y_true, y_pred)4 r_score = recall_score(y_true, y_pred)5 return p_score, r_score最后,再定义一个函数来整体实现不同阈值下精确率和召回率的计算,代码如下:
161def p_r_curve(y_true, y_scores):2 thresholds = sorted(np.unique(y_scores))3 precisions, recalls = [], []4 for thre in thresholds:5 y_pred = predict(y_scores, thre)6 r = compute_scores(y_true, y_pred)7 precisions.append(r[0])8 recalls.append(r[1])9 # 去掉召回率中末尾重复的情况10 last_ind = np.searchsorted(recalls[::-1], recalls[0]) + 111 precisions = precisions[-last_ind:]12 recalls = recalls[-last_ind:]13 thresholds = thresholds[-last_ind:]14 precisions.append(1)15 recalls.append(0)16 return precisions, recalls, thresholds在上述代码中,第2行用来从原始y_scores中得到候选阈值,并进行升序处理;第4-8行为依次遍历每个阈值并计算得到相应的精确率和召回率(注意,此时计算得到的召回率是递减的);第10-13行是先找到升序状态下recalls中最后一个元素开始重复的索引,然后再将后续相同的结果去掉,例如recalls=[1.0, 1.0, 0.75, 0.5, 0.25, 0.25, 0.25, 0.0]去重后就会变成recalls=[1.0, 0.75, 0.5, 0.25, 0.25, 0.25, 0.0],当然不去重也可以掌柜这里只是为了得到和sklearn一样的结果;第14-15行则是分别在精确率和召回率中加入初始值,便于后续作图。
之后,我们便可以通过真实标签和预测概率计算得到相应的结果:
161if __name__ == '__main__':2 y_true = np.array([0, 0, 0, 1, 1, 0, 1, 1])3 y_scores = np.array([0.5, 0.55, 0.74, 0.65, 0.28, 0.17, 0.3, 0.45])4 precision, recall, thresholds = precision_recall_curve(y_true, y_scores)5 ap = average_precision_score(y_true, y_scores)6 print("sklearn 计算结果:")7 print("precision", precision)8 print("recall", recall)9 print("thresholds", thresholds)10
11 print("\n编码实现 计算结果:")12 precision, recall, thresholds = p_r_curve(y_true, y_scores)13 ap = compute_ap(recall, precision)14 print("precision", precision)15 print("recall", recall)16 print("thresholds", thresholds)上述代码运行后的结果为:
91sklearn 计算结果:2precision [0.571428 0.5 0.4 0.25 0.333333 0.5 0. 1.]3recall [1. 0.75 0.5 0.25 0.25 0.25 0. 0. ]4thresholds [0.28 0.3 0.45 0.5 0.55 0.65 0.74]5
6编码实现 计算结果:7precision [0.571428, 0.5, 0.4, 0.25, 0.333333, 0.5, 0.0, 1]8recall [1.0, 0.75, 0.5, 0.25, 0.25, 0.25, 0.0, 0]9thresholds [0.28, 0.3, 0.45, 0.5, 0.55, 0.65, 0.74]对于AUC值的计算,采用矩形规则可以通过如下代码进行实现:
81def compute_ap(recall, precision):2 # \\text{AP} = \\sum_n (R_n - R_{n-1}) P_n3 rp = [item for item in zip(recall, precision)][::-1] # 按recall升序进行排序4 ap = 05 for i in range(1, len(rp)):6 ap += (rp[i][0] - rp[i - 1][0]) * rp[i][1]7 # print(f"({rp[i][0]} - {rp[i - 1][0]}) * {rp[i][1]}")8 return ap采用梯形规则的话可以通过sklearn中的sklearn.metrics.auc进行计算。
上述示例的AUC值计算结果为:
111if __name__ == '__main__':2 y_true = np.array([0, 0, 0, 1, 1, 0, 1, 1])3 y_scores = np.array([0.5, 0.55, 0.74, 0.65, 0.28, 0.17, 0.3, 0.45])4 ap = average_precision_score(y_true, y_scores)5 print("sklearn 计算结果:")6 print("ap", ap) # ap 0.49285714285714297 print("auc", auc(recall, precision)) # auc 0.390178571428571438 9 print("\n编码实现 计算结果:")10 ap = compute_ap(recall, precision)11 print("ap", ap) # ap 0.49285714285714294.2 结果可视化
在编码实现各个指标的计算过后,进一步便可以对其进行可视化。下面掌柜以逻辑回归二分类模型为例进行示例。
111from sklearn.datasets import load_iris2from sklearn.model_selection import train_test_split3def get_dataset():4 x, y = load_iris(return_X_y=True)5 random_state = np.random.RandomState(2020)6 n_samples, n_features = x.shape7 x = np.concatenate([x, random_state.randn(n_samples, 200 * n_features)], axis=1)8 # 针对二分类下的pr曲线9 x_train, x_test, y_train, y_test = train_test_split(10 x[y < 2], y[y < 2], test_size=0.5, random_state=random_state)11 return x_train, x_test, y_train, y_test在上述代码中,第4-7行为导入数据集并添加相应的噪音维度以便更好观察pr曲线(因为原始数据过于简单);第9-10行则是只取其中的两个类别。
进一步,可以通过如下步骤就是进行可视化:
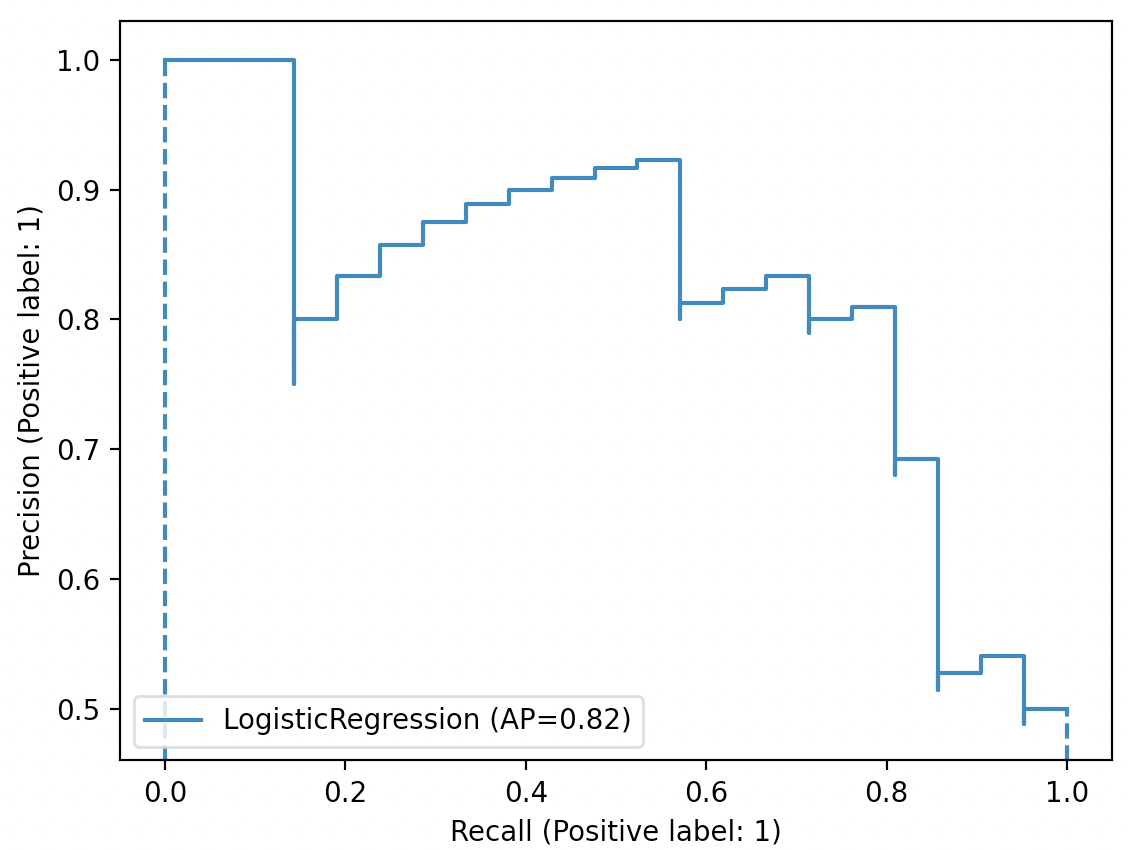
xxxxxxxxxx161from sklearn.linear_model import LogisticRegression2if __name__ == '__main__':3 x_train, x_test, y_train, y_test = get_dataset()4 model = LogisticRegression()5 model.fit(x_train, y_train)6 y_scores = model.predict_proba(x_test)7 precision, recall, _ = p_r_curve(y_test, y_scores[:, 1])8 ap = compute_ap(recall, precision)9 plt.plot(recall, precision, drawstyle="steps-post", label=f'LogisticRegression (AP={ap})')10 plt.legend(loc="lower left")11 plt.xlabel("Recall (Positive label: 1)")12 plt.ylabel("Precision (Positive label: 1)")13 14 # 通过sklear方法进行绘制15 plot_precision_recall_curve(model, x_test, y_test)16 plt.show()在上述代码中,第3-5行用来训练模型;第6-8行分别用来计算测试集的预测概率、精确率、召回率以及平均精度;第9-12行则是可视化Precision-Recall曲线,其中drawstyle参数的目的是得到阶梯状的可视化结果;第15-16行是通过sklearn中的接口进行可视化。最终两者都将得到如图3所示的结果。
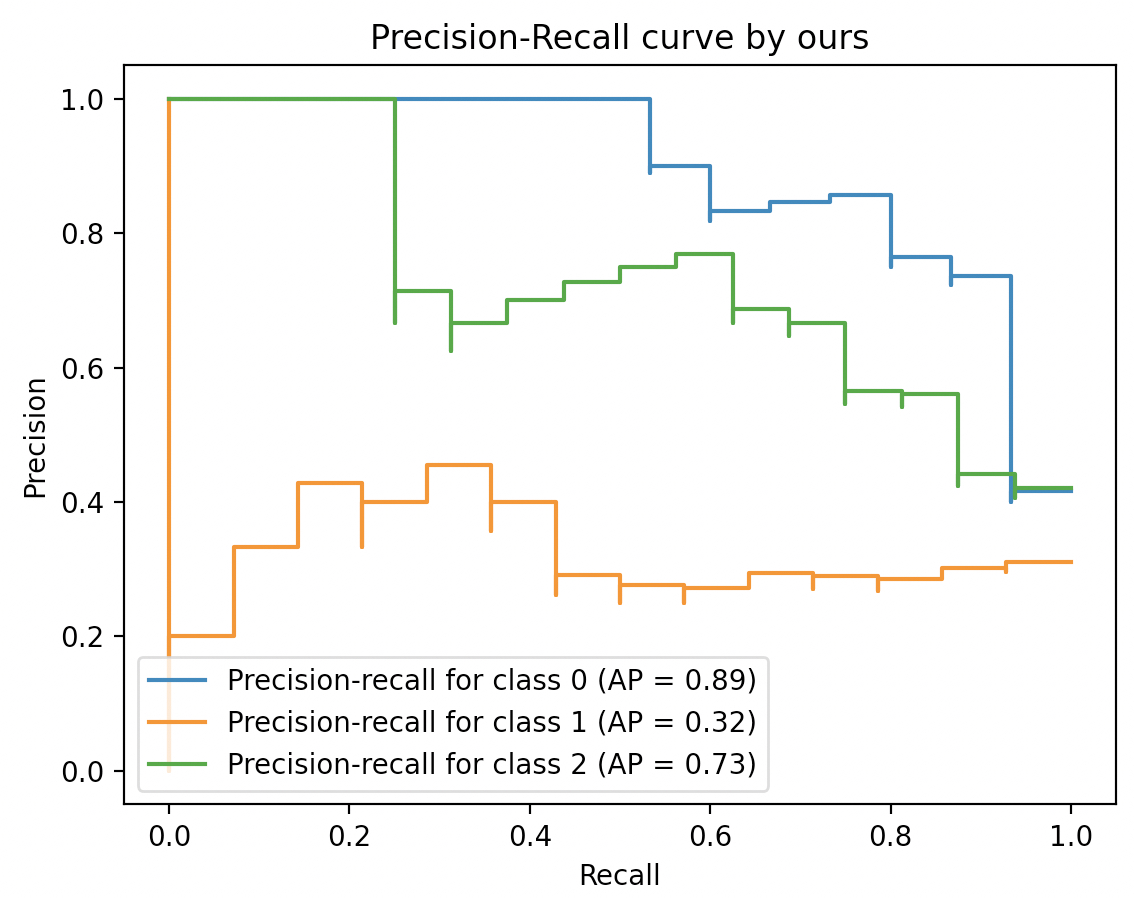
当然,除了二分类场景之外还可以在多分类场景下来可视化每个类别对应的PR曲线,示例代码如下:
xxxxxxxxxx151if __name__ == '__main__':2 x_train, x_test, y_train, y_test = get_dataset()3 model = LogisticRegression(multi_class='ovr')4 model.fit(x_train, y_train)5 b_y = label_binarize(y_test, classes=[0, 1, 2])6 y_scores = model.predict_proba(x_test)7 for i in range(len(np.unique(y_test))):8 precision, recall, _ = p_r_curve(b_y[:, i], y_scores[:, i])9 ap = compute_ap(recall, precision)10 plt.plot(recall, precision, drawstyle="steps-post", 11 label=f'Precision-recall for class {i} (AP = {ap})')12 plt.xlabel("Recall")13 plt.ylabel("Precision")14 plt.title("Precision-Recall curve by ours")15 plt.legend(loc="lower left")在上述代码中,第5行用来将原始标签转化为one-hot编码形式的标签,由于后续计算每个类别所对应的相应指标;第7-11行则是分别对每个类别的Precision-Recall曲线进行可视化。当然,也可以直接借助sklearn中的方法来完成。
xxxxxxxxxx121 # 通过sklear方法进行绘制2 _, ax = plt.subplots()3 for i in range(len(np.unique(y_test))):4 precision, recall, _ = p_r_curve(b_y[:, i], y_scores[:, i])5 ap = compute_ap(recall, precision)6 display = PrecisionRecallDisplay(7 recall=recall,8 precision=precision,9 average_precision=ap)10 display.plot(ax=ax, name=f"Precision-recall for class {i}")11 ax.set_title("Precision-Recall curve by sklearn")12 plt.show()最终,可视化后的结果如图7所示:
5 总结
在这篇文章中,掌柜首先从一个新的视角回顾了精确率与召回率的概念和原理,并且通过示例详细介绍了准确率的不足之处以及为什么需要用到精确率和准确率;接着介绍了基于精确率和召回率的Precision-Recall曲线的作用与原理;最后,掌柜详细介绍了如何编码实现召回率和精确率中各项指标的计算以及二分类和多分类场景下Precision-Recall曲线的可视化方法。
本次内容就到此结束,感谢您的阅读!如果你觉得上述内容对你有所帮助,欢迎点赞分享!若有任何疑问与建议,请添加掌柜微信nulls8(备注来源)或加群进行交流。青山不改,绿水长流,我们月来客栈见!
引用
[1]https://en.wikipedia.org/w/index.php?title=Information_retrieval&oldid=793358396#Average_precision
[2]https://en.wikipedia.org/wiki/Precision_and_recall
[5]https://scikit-learn.org/stable/auto_examples/model_selection/plot_precision_recall.html
[6]https://en.wikipedia.org/wiki/Trapezoidal_rule
[7]https://builtin.com/data-science/precision-and-recall
[8]https://en.wikipedia.org/wiki/Trapezoidal_rule
[9]https://scikit-learn.org/stable/modules/generated/sklearn.metrics.auc.html
[10] 第3章从零认识逻辑回归(附高清PDF与教学PPT)
[11] 示例代码:https://github.com/moon-hotel/MachineLearningWithMe