从基尼不纯度来看待样本的划分方式,直观上若集合D中存在样本数的类别越多,那么其对应的“不纯度”也就会越大,直观的说也就是该集合“不纯”,这也很类似于信息熵的性质。对于CART分类树的剪枝过程来说,第二步交叉验证倒是容易理解,但第一步的子序列到底是怎么来的?我什么要减去其中g(t)最小的子树?
1 引言
在上一篇文章中,笔者分别介绍了用ID3和C4.5这两种算法来生成决策树。其中ID3算法每次用信息增益最大的特征来划分数据样本,而C4.5算法每次用信息增益比最大的特征来划分数据样本。接下来,再来看另外一种采用基尼不纯度(Gini Impurity)为标准的划分方法,CART算法。
2 CART算法
分类与回归树(Classification and Regression Tree, CART),是一种既可以用于分类也可以用于回归的决策树,同时它也是应用最为广泛的决策树学习方法之一。CART假设决策树是二叉树,内部节点特征的取值均为“是”和“否”,左分支取值为“是”,右分支取值为“否”。这样,决策树在构建过程中就等价于递归地二分每个特征,将整个特征空间划分为有限个单元[1]。
在本书中,笔者暂时只对其中的分类树进行介绍。总体来说,利用CART算法来构造一棵分类需要完成两步:①基于训练数据集生成决策树,并且生成的决策树要尽可能的大;②用验证集来对已生成的树进行剪枝并选择最优子树。
2.1 分类树生成算法
在介绍分类树的生成算法前,让我们先来看一看新引入划分标准基尼不纯度。在分类问题中,假设某数据集包含有
因此,对于给定的样本集合
其中,
从基尼不纯度的定义可以看出,若集合
同时,在决策树的生成过程中,如果样本集合
则在特征
其中
在介绍完成基尼不纯度后,就能够列出CART分类树的生成步骤:
输入:训练数据集
输出:CART分类决策树。
根据训练集,从根节点开始,递归地对每个节点进行如下操作,并构建二叉决策树。
(1) 设训练集为
(2) 在所有可能的特征
(3) 对两个子节点递归的调用步骤(1)和(2),直到满足停止条件;
(4) 生成CART决策树。
其中,算法停止计算的条通常是节点中的样本点个数小于设定阈值,或样本集合的基尼不纯度小于设定阈值,亦或是没有更多特征,这一点同ID3和C4.5算法的停止条件类似。
2.2 分类树生成示例
在介绍完上述理论性的内容后,这里我们同样还是拿之前的数据集来对具体的生成过程进行详细的示例。由表8-1中的数据可知,此时的其基尼不纯度为
进一步,对于特征
同理,对于特征
进一步,对于特征
注意:每次划分时都是将样本集合划分为两个部分,即
由以上计算结果可知,使用
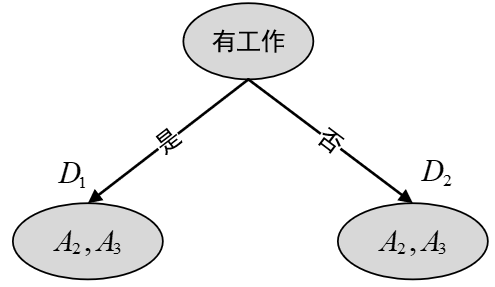
经过这次划分后,原始的样本集合就被特征“有工作”分割成了左右两个部分。接下来,再对左右两个集合递归的进行上述步骤,最终便可以得到通过CART算法生成的分类决策树,如图2所示。
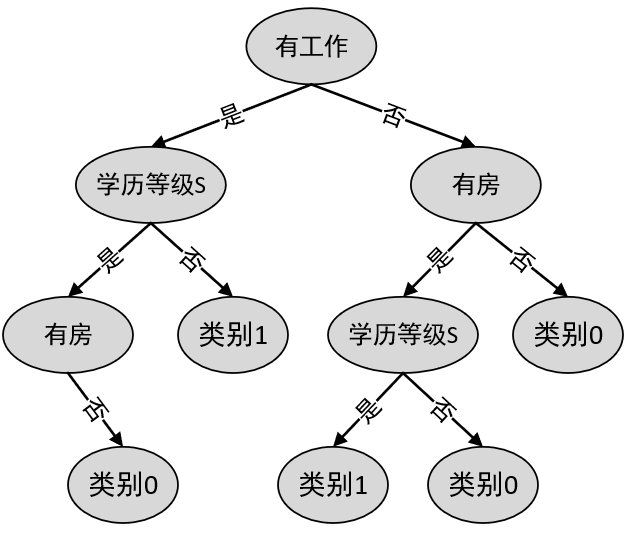
2.3 分类树剪枝步骤
在2.2节中,笔者介绍了CART中决策树的生成算法,接下来再来看看在CART中如何对生成后的决策树进行剪枝。根据第4章内容的介绍可知,总体上来说模型(决策树)越复杂,越容易产生过拟合现象,此时对应的代价函数值也相对较小。在决策树中,遇到这种情况时也就需要进行剪枝处理。CART剪枝算法由两部组成:
(1) 首先是从之前生成的决策树
(2) 然后通过交叉验证对这一子序列进行测试,从中选择最优的子树。
从上面的两个步骤可以看出,第二步并没有什么难点,关键就在于如何通过剪枝来生成这样一个决策树子序列。
剪枝,形成一个子序列
在剪枝过程中,计算子树的损失函数
其中,
具体地,从整体树
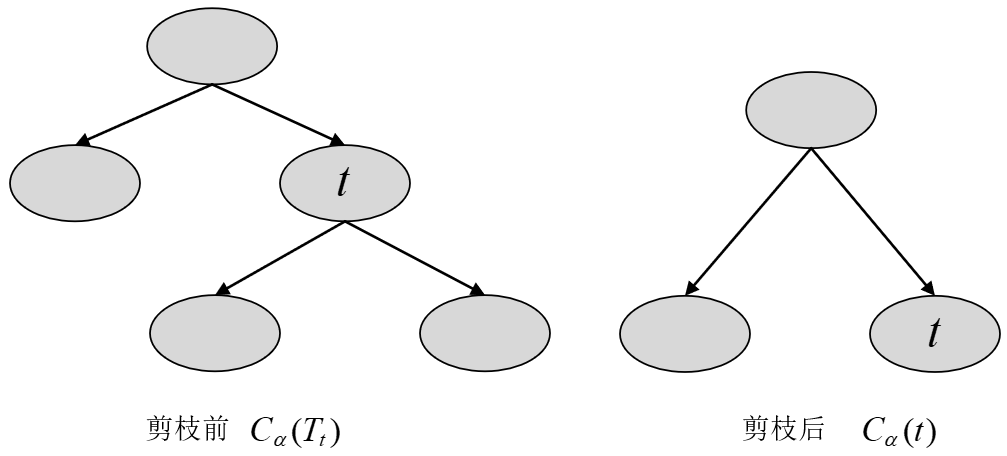
图 3. CART剪枝图 对于
同时,以
① 当
不等式成立的原因是因为,当
② 当
等式成立的原因是因为,当
③ 当
因此,当
为此,对决策树
它表示剪枝后整体损失函数减少的程度。因为每个
注意,此时得到的一系列
对于树
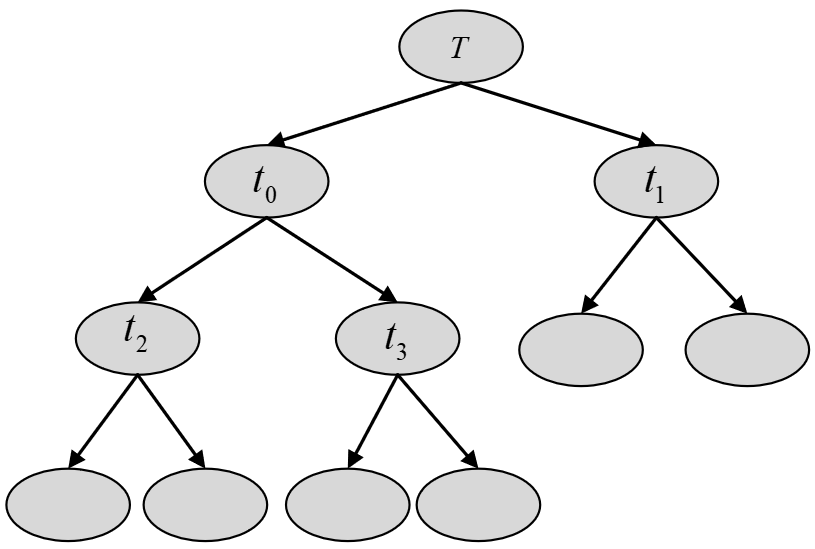
图 4. CART剪枝过程图 因此便可以计算得到
接着,在得到子树
交叉验证选择最优子树
通过上一步步我们便可以得到一系列的子树序列
进一步,CART分类树的剪枝步骤可以总结为[1]:
输入:CART算法生成的分类树
输出:最优决策树
(1) 设
(2) 设
(3) 对于树
其中,
(4) 对
(5) 令
(6) 如果
(7) 采用交叉验证在子树序列
当然,如果仅看这些步骤可能依旧会很模糊,下面笔者再通过一个简单的图示进行说明。
2.4 分类树剪枝示例
现在假设通过CART算法生成了一棵如图5所示的决策树。
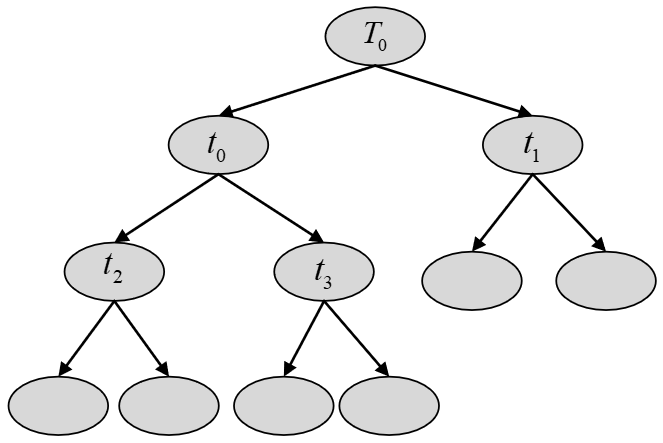
从图5可以看出,可对树
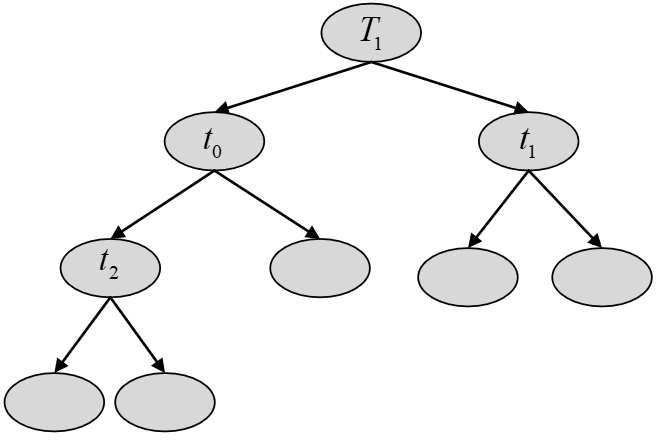
从图可以看出,根据剪枝步骤(6)可知需要再次对

从图7可以看出,根据剪枝步骤(6)可知需要再次对
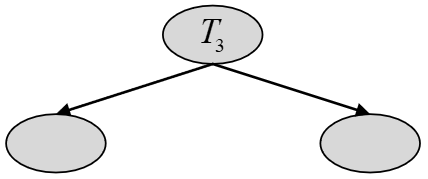
从图8可以看出,根据剪枝步骤(6)可知满足停止条件不需要继续进行剪枝。到此,便得到了整个子树序列
到此为止,对于CART决策树的整个生成与剪枝过程就介绍完了。最后,通过sklearn来完成对于CART分类树的使用也很容易,只需要将类DecisionTreeClassifier中的划分标准设置为criterion="gini"即可,其它地方依旧不变。
xxxxxxxxxx141if __name__ == '__main__':2 from sklearn.datasets import load_iris3 from sklearn.model_selection import train_test_split4
5 data = load_iris()6 x, y = data.data, data.target7 x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)8 from sklearn.tree import DecisionTreeClassifier9
10 model = DecisionTreeClassifier(criterion='gini')11 model.fit(x_train, y_train)12 print(model.score(x_test, y_test))13
14# 0.97777773 小结
在本节中,笔者首先介绍了什么是CART算法;然后进一步介绍了CART分类树中的划分标准基尼不纯度;接着详细介绍了CART分类树的生成过程,并通过一个实际例子展示整个决策树生成的计算过程;最后介绍了CART分类树剪枝过程的基本原理,并且也通过一个简单的图示展示了整个剪枝过程。
本次内容就到此结束,感谢您的阅读!如果你觉得上述内容对你有所帮助,欢迎点赞分享!若有任何疑问与建议,请添加掌柜微信nulls8(备注来源)或加群进行交流。青山不改,绿水长流,我们月来客栈见!
引用
[1] 李航,统计机器学习,清华大学出版社


