第6张朴素贝叶斯算法（附高清PDF与教学PPT）

各位朋友大家好，欢迎来到月来客栈，我是掌柜空字符。

在前4章内容中，笔者已经分别介绍了线性回归、逻辑回归、模型的改善与泛化以及K近邻算法。从这章开始，我们将继续开始学习下一个新的有监督算法模型——朴素贝叶斯（Naive Bayes, NB）。

以下为内容目录，大家可以根据需要进行定位。

6.1朴素贝叶斯算法6.1.1概念介绍6.1.2理解朴素贝叶斯6.1.3计算示例6.1.4 求解步骤6.1.5 小结6.2 贝叶斯估计6.2.1 平滑处理6.2.2 计算示例6.2.3 小结引用推荐阅读

6.1朴素贝叶斯算法

那么什么又是朴素贝叶斯呢？从名字也可以看出，朴素贝叶斯算法与贝叶斯公式有着莫大的关联，说得简单点朴素贝叶斯就是由贝叶斯公式加“朴素”这一条件所构成。

在看贝叶斯算法的相关内容时，相信各位读者一定会被突如其来的数学概念搞得头昏脑胀。比如先验概率(Prior Probability)、后验概率(Posteriori Probability,) 极大似然估计(Maximum Likelihood Estimation )，极大后验概率估计(Maximum A Posteriori Estimation)，等。所以下面，笔者将先简单的介绍一下这几个概念，让读者先对这部分内容有一个感性的认识，然后再继续介绍后面的内容。

6.1.1概念介绍

1) 先验概率

所谓先验概率指的就是根据历史经验得出来的概率。例如可以通过西瓜的颜色、敲的声音来判断其是否成熟。因为你已经有了通过颜色和声音来判断的“经验”，不管这个经验是你自己学会的还是别人告诉你的。又如在某2分类数据集中，其中正样本有4个，负样本有6个，那么通过这个数据集能够学习到的先验知识便是任取一个样本，其为正样本的可能性为40%，为负样本的可能性为60%。最后举个例子，假如办公室失窃了，理论上每个人都可能是小偷。但可以根据对每个人的了解分析得出一个可能性，比如张三偷窃的可能性为20%，李四偷窃的可能性为30%，王五偷窃的可能性为50%，而这就被称之为先验概率，它是通过历史经验得来的。

2) 后验概率

所谓后验概率指的就是通过贝叶斯公式推断得到的结果。例如上述例子中，不可能因为负样本出现的可能性为60%就判定任意取出的样本为负样本；也不能因为王五偷窃的可能性最大就判定每次办公室失窃都是他所为。先验知识只能帮助我们先取得一个大致的判断，而事实情况需要根据先验概率和条件概率来进行计算。

3) 极大后验概率估计

一言以蔽之，极大后验概率指的是在所有后验概率中选择其中最大的一个。例如上述例子中，根据先验概率和条件概率便可以计算出每个样本属于正样本还是负样本的后验概率。最后在判断该样本属于何种类别时，挑选后验概率最大的类别即可。

4) 极大似然估计

3.4.3节 $(6.1)$ 即可。

\left( \begin{matrix} 10 \\ 4 \\ \end{matrix} \right){{p}^{4}}{{(1-p)}^{6}}\;\;\;\;\;\;\;\;\;(6.1)

$p$ 为属于正样本的概率。

6.1.2理解朴素贝叶斯

由贝叶斯公式可知

P(B|A)=\frac{P(AB)}{P(A)}\;\;\;\;\;\;\;\;(6.2)

$B$ $A$ $A$ $B$ $A$ $A,B$ $P(AB)$ $P(A)$ $P(B|A)$ $(6.2)$ 转换为

P(B|A)=\frac{P(B)P(A|B)}{P(A)}\;\;\;\;\;\;\;\;(6.3)

$\mathcal{X}\subseteq R^n$ $n$ $\mathcal{Y}=\{{{c}_{1}},{{c}_{2}},...,{{c}_{K}}\}$ $x\in\mathcal{X}$ $y\in \mathcal{Y}$ $X$ $\mathcal{X}$ $Y$ $\mathcal{Y}$ $X$ $m\times n$ $y$ $P(X,Y)$ $X$ $Y$ $T=\{({{x}_{1}},{{y}_{1}}),({{x}_{2}},{{y}_{2}}),...,({{x}_{m}},{{y}_{m}})\}$ $P(X,Y)$ 独立同分布产生。

P(Y={{c}_{k}})=\frac{\#{{c}_{k}}}{m},k=1,2,...,K\;\;\;\;\;\;\;\;\;(6.4)

$\#{{c}_{k}}$ $m$ 表示样本总数。

同时，对于已知类标下的条件概率分布为

P(X=x|Y={{c}_{k}})=P({{X}^{(1)}}={{x}^{(1)}},...,{{X}^{(n)}}={{x}^{(n)}}|Y={{c}_{k}})\;\;\;\;\;\;\;\;(6.5)

${{x}^{(i)}}$ $i$ 个特征的取值。

$(6.5)$ $P(AB|D)=P(A|D)P(B|D)$ $(6.5)$ 可改写为

P(X=x|Y={{c}_{k}})=\prod\limits_{i=1}^{n}{P}({{X}^{(i)}}={{x}^{(i)}}|Y={{c}_{k}})\;\;\;\;\;\;\;\;(6.6)

$(6.3)$ $X=x$ $Y=c_k$ 的后验概率为

P(Y={{c}_{k}}|X=x)=\frac{P(X=x|Y={{c}_{k}})P(Y={{c}_{k}})}{\sum\limits_{k=1}^{K}{P}(X=x|Y={{c}_{k}})P(Y={{c}_{k}})}\;\;\;\;\;\;\;\;(6.7)

$(6.6)$ $(6.7)$ 可得

P(Y={{c}_{k}}|X=x)=\frac{P(Y={{c}_{k}})\prod\limits_{i=1}^{n}{P}({{X}^{(i)}}={{x}^{(i)}}|Y={{c}_{k}})}{\sum\limits_{k=1}^{K}{P}(Y={{c}_{k}})\prod\limits_{i=1}^{n}{P}({{X}^{(i)}}={{x}^{(i)}}|Y={{c}_{k}})}\;\;\;\;\;\;\;\;(6.8)

于是，朴素贝叶斯分类器可以表示为

y=\underset{{{c}_{k}}}{\mathop{\arg \max }}\,=\frac{P(Y={{c}_{k}})\prod\limits_{i=1}^{n}{P}({{X}^{(i)}}={{x}^{(i)}}|Y={{c}_{k}})}{\sum\limits_{k=1}^{K}{P}(Y={{c}_{k}})\prod\limits_{i=1}^{n}{P}({{X}^{(i)}}={{x}^{(i)}}|Y={{c}_{k}})}\;\;\;\;\;\;\;\;\;(6.9)

$c_k$ $(6.9)$ $(6.9)$ 可进一步简化为

y=\underset{{{c}_{k}}}{\mathop{\arg \max }}\,P(Y={{c}_{k}})\prod\limits_{i=1}^{n}{P}({{X}^{(i)}}={{x}^{(i)}}|Y={{c}_{k}})\;\;\;\;\;\;\;\;(6.10)

$\arg {{\max }_{{{c}_{k}}}}$ $y$ $c_k$ 的取值

虽然朴素贝叶斯算法看似做了一个及其简单的假设，但是其在实际的运用过程中却都有着不错的效果，尤其是在文档分类和垃圾邮件分类场景下仅需要少量数据集就能获得不错的效果[1]。

6.1.3计算示例

通过6.1.2节内容的介绍，朴素贝叶斯算法的整个原理过程就算是介绍完了。下面再来通过一个实际的计算示例来体会一下朴素贝叶斯分类器的计算流程。

$X^{(1)}\in A_1=\{0,1\}$ $X^{(2)}\in A_2=\{0,1\}$ ${{X}^{(3)}}\in {{A}_{3}}=\{D,S,T\}$ $Y\in C=\{0,1\}$ $x=(0,1,D)$ $Y$ 。

表6-1示例计算数据

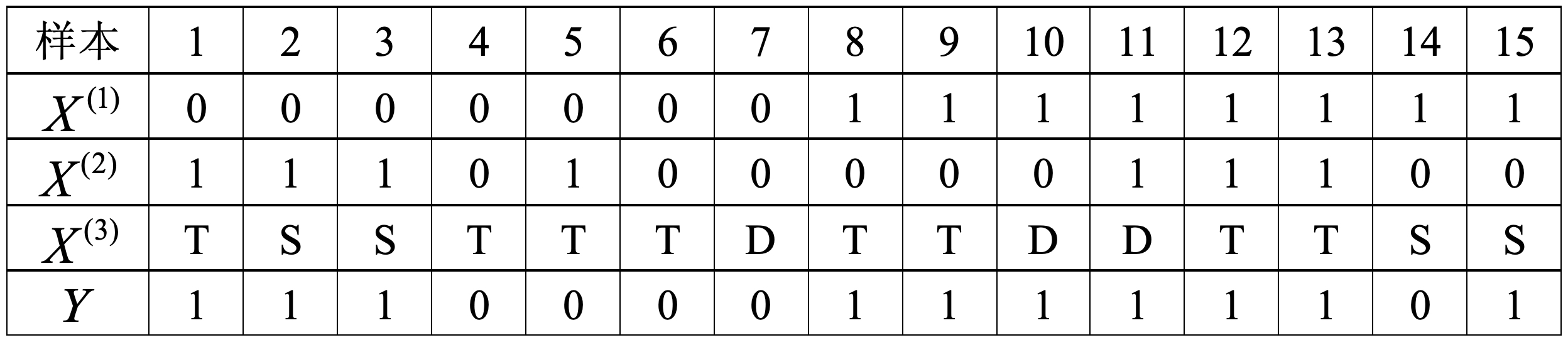
$(6.4)$ ，由表6-1易知，各个类别的先验概率为

P(Y=0)=\frac{5}{15},\ \ P(Y=1)=\frac{10}{15}\;\;\;\;\;\;\;\;\;(6.11)

条件概率为

\begin{aligned} & P({{X}^{(1)}}=0|Y=0)=\frac{4}{5},P({{X}^{(1)}}=1|Y=0)=\frac{1}{5} \\ & P({{X}^{(2)}}=0|Y=0)=\frac{4}{5},P({{X}^{(2)}}=1|Y=0)=\frac{1}{5} \\ & P({{X}^{(3)}}=D|Y=0)=\frac{1}{5},P({{X}^{(3)}}=S|Y=0)=\frac{1}{5} \\ & P({{X}^{(3)}}=T|Y=0)=\frac{3}{5},P({{X}^{(1)}}=0|Y=1)=\frac{3}{10} \\ & P({{X}^{(1)}}=1|Y=1)=\frac{7}{10},P({{X}^{(2)}}=0|Y=1)=\frac{4}{10} \\ & P({{X}^{(2)}}=1|Y=1)=\frac{6}{10},P({{X}^{(3)}}=D|Y=1)=\frac{2}{10} \\ & P({{X}^{(3)}}=S|Y=1)=\frac{3}{10},P({{X}^{(3)}}=T|Y=1)=\frac{5}{10} \\ \end{aligned} \;\;\;\;\;\;\;\;(6.12)

$x=(0,1,D)$ 进行预测。

$(6.10)$ 分别计算出其属于各个类别的后验概率为

\begin{aligned} & P(Y=0|X=x) \\ & =P(Y=0)\cdot P({{X}^{(1)}}=0|Y=0)\cdot P({{X}^{(2)}}=1|Y=0)\cdot P({{X}^{(3)}}=D|Y=0) \\ & =\frac{5}{15}\cdot \frac{4}{5}\cdot \frac{1}{5}\cdot \frac{1}{5}=\frac{4}{375} \\ \end{aligned}\;\;\;\;\;\;\;(6.13)

\begin{aligned} & P(Y=1|X=x) \\ & =P(Y=1)\cdot P({{X}^{(1)}}=0|Y=1)\cdot P({{X}^{(2)}}=1|Y=1)\cdot P({{X}^{(3)}}=D|Y=1) \\ & =\frac{10}{15}\cdot \frac{3}{10}\cdot \frac{6}{10}\cdot \frac{2}{10}=\frac{3}{125} \\ \end{aligned} \;\;\;\;\;\;\;(6.14)

$x=(0,1,D)$ $y=1$ 的可能性最大。

6.1.4 求解步骤

根据上面两节的介绍，可以将朴素贝叶斯分类算法的求解步骤总结如下：

输入： $T=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}$ ${{x}_{i}}={{(x_{i}^{(1)},x_{i}^{(2)},...,x_{i}^{(n)})}^{T}}$ $x_{i}^{(j)}$ $i$ $j$ $x_i^{(j)}\in\{a_{j1},a_{j2},...,a_{jS_j}\}$ $a_{jl}$ $j$ $l$ $j=1,2,...,n$ $l=1,2,...,S_j$ ${{y}_{i}}\in \{{{c}_{1}},{{c}_{2}},...,{{c}_{K}}\}$ $x$ ;

输出： $x$ 的分类[2]。

1) 计算先验概率与条件概率

根据极大似然估计，用给定的数据集来计算各类别的先验概率和条件概率。

P(Y={{c}_{k}})=\frac{\sum\limits_{i=1}^{m}{I}({{y}_{i}}={{c}_{k}})}{m},k=1,2,...,K\;\;\;\;\;\;\;(6.15)

\begin{aligned} & P({{X}^{(j)}}={{a}_{jl}}|Y={{c}_{k}})=\frac{\sum\limits_{i=1}^{m}{I}(x_{i}^{(j)}={{a}_{jl,}}{{y}_{i}}={{c}_{k}})}{\sum\limits_{i=1}^{m}{I}({{y}_{i}}={{c}_{k}})} \\ & j=1,2,...,n;\ \ l=1,2,...,{{S}_{j}};\ \ k=1,2,...,K \\ \end{aligned}\;\;\;\;\;\;\;\;(6.16)

$I(\cdot)$ $y_i=c_k$ 时输出值为1，反之则为0。

2) 计算各特征取值下的后验概率

P(Y={{c}_{k}})=\prod\limits_{j=1}^{n}{P}({{X}^{(j)}}={{x}^{(j)}}|Y={{c}_{k}}),k=1,2,...,K\;\;\;\;\;\;\;(6.17)

3) 极大化后验概率确定类别

y=\underset{{{c}_{k}}}{\mathop{\arg \max }}\,P(Y={{c}_{k}})\prod\limits_{j=1}^{n}{P}({{X}^{(j)}}={{x}^{(j)}}|Y={{c}_{k}})\;\;\;\;\;\;\;(6.18)

到此，对于朴素贝叶斯算法的原理及计算过程就介绍完了。根据6.1.4节的介绍可以知道，朴素贝叶斯算法所接受的特征输入都是离散型特征（Discrete Features），也就非连续性的特征取值，例如基于词袋模型的文本特征表示等。因此，对于这部分的示例代码将放在第7章中进行介绍。

6.1.5 小结

在本节中，笔者首先介绍了朴素贝叶斯算法中的几个基本概念；然后详细介绍了朴素贝叶斯算法的原理，知道了“朴素”一词的含义以及为什么可以通过贝叶斯算法来完成分类任务；最后对朴素贝叶斯算法的具体计算流程进行了总结。

6.2 贝叶斯估计

$P({{X}^{(3)}}=D|Y=1)=0$ ，即训练集中不存在这一情况，而在测试的数据样本中却存在这种情况。如果此时仍旧将这种情况下的条件概率看作是是0，那么在预测的时候将会产生很大的错差。面对这样的情况该怎么办呢？

6.2.1 平滑处理

通常，解决这类问题的一个有效办法就是在各个估计中加入一个平滑项（Smoothing Parameter）。那么，此时先验概率和条件概率的计算方法为

{{P}_{\lambda }}(Y={{c}_{k}})=\frac{\sum\limits_{i=1}^{m}{I}({{y}_{i}}={{c}_{k}})+\lambda }{m+K\lambda }\;\;\;\;\;\;\;\;(6.19)

{{P}_{\lambda }}({{X}^{(j)}}={{a}_{jl}}|Y={{c}_{k}})=\frac{\sum\limits_{i=1}^{m}{I}(x_{i}^{(j)}={{a}_{jl,}}{{y}_{i}}={{c}_{k}})+\lambda }{\sum\limits_{i=1}^{m}{I}({{y}_{i}}={{c}_{k}})+{{S}_{j}}\lambda }\;\;\;\;\;\;\;\;(6.20)

$K$ $S_j$ $j$ $\lambda\geq0$ $\lambda=1$ 时称为拉普拉斯平滑（Laplace Smoothing），这也是常用的做法。

$\lambda >0$ $(6.19)$ $(6.20)$ $\lambda=0$ 时，就是极大似然估计；

6.2.2 计算示例

$\lambda=1$ $K=2$ $S_1=2,S_2=2,S_3=3$ 。

$(6.19)$ 易知，各类别的先验概率分别为

P(Y=0)=\frac{6}{17},\ \ P(Y=1)=\frac{11}{17}\;\;\;\;\;\;\;(6.21)

条件概率为

\begin{aligned} & P({{X}^{(1)}}=0|Y=0)=\frac{5}{7},P({{X}^{(1)}}=1|Y=0)=\frac{2}{7} \\ & P({{X}^{(2)}}=0|Y=0)=\frac{5}{7},P({{X}^{(2)}}=1|Y=0)=\frac{2}{7} \\ & P({{X}^{(3)}}=D|Y=0)=\frac{2}{8},P({{X}^{(3)}}=S|Y=0)=\frac{2}{8} \\ & P({{X}^{(3)}}=T|Y=0)=\frac{4}{8},P({{X}^{(1)}}=0|Y=1)=\frac{4}{12} \\ & P({{X}^{(1)}}=1|Y=1)=\frac{8}{12},P({{X}^{(2)}}=0|Y=1)=\frac{5}{12} \\ & P({{X}^{(2)}}=1|Y=1)=\frac{7}{12},P({{X}^{(3)}}=D|Y=1)=\frac{3}{13} \\ & P({{X}^{(3)}}=S|Y=1)=\frac{4}{13},P({{X}^{(3)}}=T|Y=1)=\frac{6}{13} \\ \end{aligned}\;\;\;\;\;\;\;(6.22)

计算出属于各个类别的后验概率为

\begin{aligned} & P(Y=0|X=x) \\ & =P(Y=0)\cdot P({{X}^{(1)}}=0|Y=0)\cdot P({{X}^{(2)}}=1|Y=0)\cdot P({{X}^{(3)}}=D|Y=0) \\ & =\frac{6}{17}\cdot \frac{5}{7}\cdot \frac{2}{7}\cdot \frac{2}{8}\approx 0.02 \\ \end{aligned} \;\;\;\;\;\;\;\;(6.23)

\begin{aligned} & P(Y=1|X=x) \\ & =P(Y=1)\cdot P({{X}^{(1)}}=0|Y=1)\cdot P({{X}^{(2)}}=1|Y=1)\cdot P({{X}^{(3)}}=D|Y=1) \\ & =\frac{11}{17}\cdot \frac{4}{12}\cdot \frac{7}{12}\cdot \frac{3}{13}\approx 0.03 \\ \end{aligned}\;\;\;\;\;\;\;\;(6.24)

$x=(0,1,D)$ $y=1$ 的可能性最大。

到此，对于朴素贝叶斯算法的原理及计算过程就介绍完了。对于这部分的sklearn示例代码也将在第7章中进行介绍。由于在不同的书中对于一些算法原理有着不同的称谓，这也导致读者在初学翻阅各种资料时候发现一会儿又多了这个概念，一会儿又多了那个概念极为苦恼。不过名称并不太重要，重要的是要知道具体指代的具体东西。如图6-1所示是笔者对遇到的各种“叫法”进行的总结，仅供参考。

图6-1 概念辨析图

6.2.3 小结

在本节中，笔者介绍了如何处理在贝叶斯算法中条件概率为0时的处理方法，即贝叶斯估计；然后也辨析了几个在贝叶斯算法中容易混淆的概念。值得一提的是，其实平滑处理这种做法不仅仅可以用于此处，在其它任何类似的情况中都可以借鉴这种做法。例如在下一章将要介绍的TF-IDF中同样也会用到。亦或是编写含有除运算的程序中，为了防止分母出现零的情况，都可以采用这样的做法。

总结一下，在本章中笔者首先介绍了朴素贝叶斯算法中的几个基本概念，包括先验概率、后验概率、极大后验概率和极大似然估计等，因为只有在对这些概率有了感性的认识才更加有利于对后续算法原理的理解；接着笔者介绍了朴素贝叶斯算法的基本原理，并且还以一个真实的示例对整个算法计算过程进行了演示；然后介绍了以平滑处理的方式来处理贝叶斯算法中可能存在的条件概率为0的情况，即贝叶斯估计；最后还对贝叶斯算法中几种常见的算法名称进行了总结。

本次内容就到此结束，感谢您的阅读！如果你觉得上述内容对你有所帮助，欢迎分享至一位你的朋友！若有任何疑问与建议，请添加笔者微信'nulls8'或加群进行交流。青山不改，绿水长流，我们月来客栈见！

引用

[1]Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825-2830, 2011.

[2]李航，统计机器学习，清华大学出版社

第6张朴素贝叶斯算法（附高清PDF与教学PPT）

于2021年12月11日2021年12月11日由空字符发布

6.1朴素贝叶斯算法

6.1.1概念介绍

6.1.2理解朴素贝叶斯

6.1.3计算示例

6.1.4 求解步骤

6.1.5 小结

6.2 贝叶斯估计

6.2.1 平滑处理

6.2.2 计算示例

6.2.3 小结

引用

推荐阅读

Sklearn学习指南

详解机器学习中的Precision-Recall曲线

Sklearn学习指南

集成学习与随机森林

机器学习

CART生成与剪枝算法

第6张 朴素贝叶斯算法（附高清PDF与教学PPT）

于2021年12月11日2021年12月11日由 空字符 发布

6.1朴素贝叶斯算法

6.1.1概念介绍

6.1.2理解朴素贝叶斯

6.1.3计算示例

6.1.4 求解步骤

6.1.5 小结

6.2 贝叶斯估计

6.2.1 平滑处理

6.2.2 计算示例

6.2.3 小结

引用

推荐阅读

相关文章

Sklearn学习指南

详解机器学习中的Precision-Recall曲线

Sklearn学习指南

集成学习与随机森林

机器学习

CART生成与剪枝算法

第6张朴素贝叶斯算法（附高清PDF与教学PPT）

于2021年12月11日2021年12月11日由空字符发布