集成学习与随机森林

通过前面几章的学习，我们已经了解了机器学习中的多种分类和回归模型。现在有一个问题就是，这么多模型哪一个最好呢？以分类任务为例，当拿到一个实际的数据集时，如果是你你会选择哪种模型进行建模呢？一个狡猾的办法就是挨个都试一下，那这样做有没有道理呢？还别说，在实际的情况中真的可能会都去试一下。假如现在选择A、B、C这三个模型进行建模，最后得到结果是：A的分类准确率为0.93，B的分类准确率为0.95，C的准确率为0.88。那最终应该选择哪一个模型呢？是模型B吗？

1 引言

各位朋友好，欢迎来到月来客栈，我是掌柜空字符。

随机森林可能是一个很多人多听过或者使用过的机器学习模型，那随机森林背后的思想与原理又是怎么样的呢？他和集成学习之间又有着什么样的联系？

接下来的这篇文章，让掌柜带着大家来逐一回答上述问题。

2 集成学习

2.1 集成学习思想

假设现在一共有100个样本，其标签为二分类（正、负两类），三个模型的部分分类结果如表1所示。

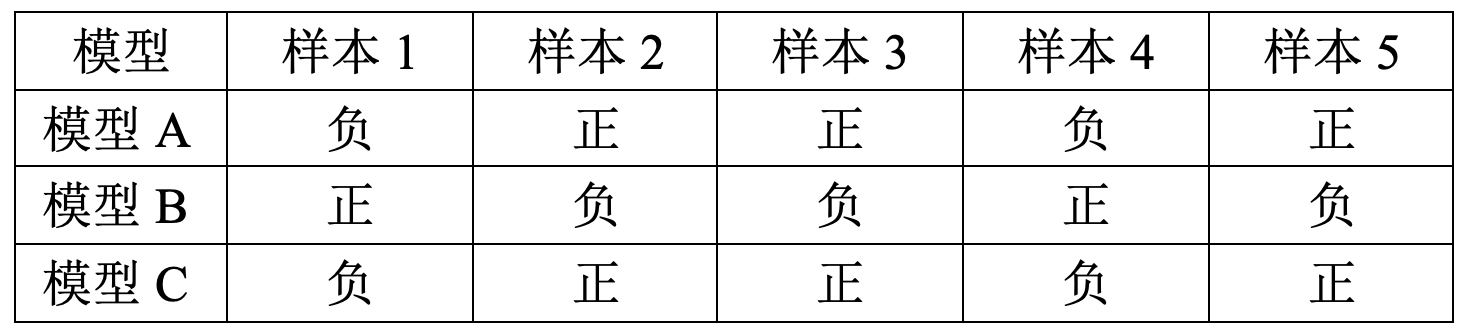
在表1中的5个样本，模型A和C均能分类正确，而模型B不能分类正确。但如果此时将这三个模型一起用于分类任务的预测，并且对于每一个样本的最终输出结果采用基于投票的规则在三个模型的输出结果中进行选择。例如表8-6中的第1个样本，模型A和C均判定为“负类”只有B判定为“正类“，则最后的输出便为”负类“。那么此时，我们就有可能得到一个分类准确率为1的“混合”模型。

注意：在其余的95个样本中，假设根据投票规则均能分类正确。

2.2 集成学习种类

在机器学习中，基于这种组合思想来提高模型精度的方法被称为集成学习（Ensemble Learning）。俗话说“三个臭皮匠，赛过诸葛亮”，这句话就完美阐述了集成学习的潜在思想——通过将多个模型结合在一起来提高整体的泛化能力[2]。

常见的集成模型主要包括以下三种：

1) Bagging集成学习

Bagging的核心思想为并行地训练一系列各自独立的同类模型，然后再将各个模型的输出结果按照某种策略进行组合，并输出最终结果。例如分类中可采用投票策略，回归中可采用平均策略。通常来说，模型越容易过拟合，则越适用于Bagging集成学习方法。

2) Boosting集成学习

Boosting的核心思想为先串行地训练一系列前后依赖的同类模型，即后一个模型用来对前一个模型的输出结果进行修正，最后再通过某种策略将所有的模型组合起来，并输出最终的结果。通常来说，模型越容易欠拟合，则越适用于Boosting集成学习方法。

3) Stacking集成学习

Stacking的核心思想为并行地训练一系列各自独立的不同类模型，然后再将各个模型的输出结果作为输入来训练一个新模型（例如：逻辑回归），并通过这个新模型来输出最终预测的结果[2]。通常来说，Stacking集成学习也适用于欠拟合的机器学习模型。

下面的内容，掌柜就来大致介绍一下各类集成模型中常见的算法和使用示例。

2.3 Bagging集成学习

Bagging的全称为 Bootstrap Aggregation，而这两个单词也分别代表了Bagging在执行过程中的两个步骤，①Bootstrap Samples；②Aggregate Outputs。总结起来就是Bagging首先从原始数据中随机抽取多组包含若干数量样本的子训练集，以及对于各子训练集来说再随机抽取若干特征维度作为模型输入；然后分别以不同的子训练集来训练得到不同的基模型，同时将各个模型的预测结果进行聚合，即

其中$M$$M$表示基模型的数量，$f_m(x)$$f_m(x)$表示不同的基模型。

同时，由于Bagging的策略是取所有基模型的“平均”值作为最终模型的输出结果，所以Bagging集成方法能够很好的降低模型高方差（过拟合）的情况。因此通常来说，在使用Bagging集成方法的时候，可以尽量使得每个基模型都出现过拟合的现象。下面，掌柜就来介绍在 sklearn中如何使用Bagging集成学习方法。

1) Bagging on KNN

在sklearn中，可以通过from sklearn.ensemble import BaggingClassifier来导入Bagging集成学习方法中的分类模型。下面先来介绍一下BaggingClassifier类中常见的重要参数及其含义。

xxxxxxxxxx
8
1
1 def __init__(self,
2
2     base_estimator=None,
3
3     n_estimators=10,
4
4     max_samples=1.0,
5
5     max_features=1.0,
6
6     bootstrap=True,
7
7     bootstrap_features=False,
8
8     n_jobs=None): 

上述代码是类BaggingClassifier初始化方法中的部分参数，其中base_estimator表示所使用的基模型；n_estimators表示需要同时训练多少个基模型；max_samples表示每个子训练集中最大的样本数量，其可以是整数也可以是0到1之间的浮点数（此时表示在总样本数中的占比）；max_features表示子训练集中特征维度的数量（由于是随机抽样，所以不同的子训练集特征维度可能不一样）；bootstrap=True表示在同一子训练集中同一样本可以重复抽样出现；bootstrap_features=False表示在同一子训练集中同一特征维度不能重复出现（如果设置为True，极端情况下所有的特征维度可能都一样）；n_jobs表示同时要使用多个CPU核并行进行计算。

下面以KNN作为基模型通过sklearn中的BaggingClassifier类来进行Bagging集成学习建模，完整代码见Chapter08/02_ensemble_bagging_knn.py文件。

xxxxxxxxxx
9
1
1 bagging = BaggingClassifier(KNeighborsClassifier(n_neighbors=3),
2
2                                 n_estimators=5,
3
3                                 max_samples=0.8,
4
4                                 max_features=3,
5
5                                 bootstrap_features=False,
6
6                                 bootstrap=True)
7
7 bagging.fit(x_train, y_train)
8
8 print(bagging.estimators_features_)
9
9 print(bagging.score(x_test, y_test))

在上述代码中，第1行表示使用了KNN作为基模型，且K值设置为了3；第2-3行分别表示一共采用了5个KNN分类器，每个分类器在进行训练时使用原始训练集80%的样本进行训练；第4-5行表示每个子训练集的仅使用其中3个特征维度（一共又4个），且不能重复；第6行表示每个子训练集在划分样本时可以重复。

训练完成后可以得到如下结果：

xxxxxxxxxx
2
1
1 [array([1,3,0]),array([0,1,2]),array([3,1,2]),array([0,1,2]),array([1,3,0])]
2
2 0.9777

其中[1, 3, 0]表示该模型在训练时使用的是第1、3和0个特征维度，其它同理。

2) Bagging on Decision Tree

正如上面介绍到，在通过Bagging方法进行集成学习时其基模型可以是其它任意模型，所以自然而然也可以是决策树。同时，由于对决策树使用Bagging集成方法是一个较为热门的研究方向，因此它还有另外一个响亮的名字随机森林（Random Forests）。根据Bagging的思想来看，随机森林这个名字也很贴切，一系列的树模型就变成了森林。在sklearn中，如果是通过类BaggingClassifier来实现Bagging集成学习，当参数base_estimator=None时，默认就会采用决策树作为基模型。由于这部分的内容较多且应用也比较广泛，所以详细内容将会单独放在第3节中进行介绍。

2.4 Boosting集成学习

Boosting同Bagging一样，都是用于提高模型的泛化能力。不同的是Boosting方法是通过串行地训练一系列模型来达到这一目的。在Boosting集成学习中，每个基模型都会对前一个基模型的输出结果进行改善。如果前一个基模型对某些样本进行了错误的分类，那么后一个基模型就会针对这些错误的结果进行修正。这样在经过一系列串行基模型的拟合后，最终就会得到一个更加准确的结果。因此， Boosting集成学习方法经常被用于改善模型高偏差的情况（欠拟合现象）。

在Boosting集成学习中最常见的算法就是AdaBoost，关于该算法的具体原理掌柜在这里就暂不阐述，各位读者朋友要是兴趣可以自行去查找相关资料。下面直接来看AdaBoost算法在sklearn中的用法。

在sklearn中，可以通过from sklearn.ensemble import AdaBoostClassifier来导入AdaBoosting集成学习方法中的分类模型。下面先来介绍一下AdaBoostClassifier类中常见的重要参数及其含义。

xxxxxxxxxx
4
1
1 def __init__(self,
2
2     base_estimator=None,
3
3     n_estimators=50,
4
4     learning_rate=1.):

上述代码是类BaggingClassifier初始化方法中的部分参数，其中base_estimator表示所使用的基模型，如果设置未None则模型使用决策树；n_estimators表示基模型的数量，默认为50个；learning_rate用来控制每个基模型的贡献度，默认为1即等权重。

下面以决策树作为基模型通过sklearn中的AdaBoostClassifier类来进行Boosting集成学习建模，完整代码见Chapter08/ 03_AdaBoosting.py文件。

xxxxxxxxxx
5
1
1 x_train, x_test, y_train, y_test = load_data()
2
2 dt = DecisionTreeClassifier(criterion='gini', max_features=4, max_depth=1)
3
3 model = AdaBoostClassifier(base_estimator=dt, n_estimators=100)
4
4 model.fit(x_train, y_train)
5
5 print("模型在测试集上的准确率为：", model.score(x_test, y_test)) # 1.0

在上述代码中，第2行表示定义决策树基模型；第3行表示定义AdaBoost分类器，并将决策树基模型作为参数传入到类AdaBoostClassifier中。

到此，对于AdaBoost的示例用法就介绍完了。不过细心的读者可能会问，此时基分类器决策树和AdaBoost均有自己的超参数，如果要在上述训练过程中使用网格搜索GridSearchCV该怎么操作呢？关于这部分内容掌柜在此就不做介绍，可以直接参见Chapter08/04_AdaBoosting_gridsearch.py文件。

2.5 Stacking集成学习

不同于Bagging和Boosting这两种集成学习方法，Stacking集成学习方法首先通过训练得到多个基于不同算法的基模型，然后再将通过训练一个新模型来对其它模型的输出结果进行组合。例如选择以逻辑回归和KNN作为基模型，以决策树作为组合模型。那么Stacking集成方法的做法为：首先将训练得到前两个基模型；然后再以基模型的输出作为决策树的输入训练组合模型；最后以决策树的输出作为真正的预测结果。

在sklearn中，可以通过如下代码来导入StackingClassifier集成学习方法中的分类模型。

xxxxxxxxxx
1
1
from sklearn.ensemble import StackingClassifier

下面先来介绍一下StackingClassifier类中常见的重要参数及其含义。

xxxxxxxxxx
4
1
1 def __init__(self, 
2
2     estimators, 
3
3     final_estimator=None,
4
4     passthrough=False)

上述代码是类StackingClassifier初始化方法中的部分参数，其中estimators表示所使用的基模型；final_estimator表示最后使用的组合模型；当passthrough=False时，表示在训练最后的组合模型时只将各个基模型的输出作为输入，当passthrough=True时表示同时也将原始样本也作为输入。

下面以逻辑回归、K近邻作为基模型，决策树作为组合模型，并通过sklearn中的StackingClassifier类来进行Stacking集成学习建模，完整代码见Chapter08/ 05_ensemble_stacking.py文件。

xxxxxxxxxx
7
1
1 estimators = [('logist', LogisticRegression(max_iter=500)),
2
2               ('knn', KNeighborsClassifier(n_neighbors=3))]
3
3 stacking = StackingClassifier(estimators=estimators,
4
4                               final_estimator=DecisionTreeClassifier())
5
5 stacking.fit(x_train, y_train)
6
6 acc = stacking.score(x_test, y_test)
7
7 print("模型在测试集上的准确率为：", acc)#0.956

在上述代码中，第1-2行分别用来定义两个基模型，并进行相应的初始化；第3-4行用来定义Stacking分类器，并指定组合模型为决策树。

到此，对于sklearn中Stacking集成学习的示例用法就介绍完了。同时，上述训练过程的网格搜索示例用法可以参见Chapter08/06_ensemble_stacking_gridsearch.py文件。

3 随机森林

3.1 随机森林原理

正如掌柜在第8.6.3节中介绍的那样，随机森林本质上也就是基于决策树的Bagging集成学习模型。因此，随机森林的建模过程总体上可以分为三步[3]：

第一步，对原始数据集进行随机采样，得到多个训练子集；

第二步，在各个训练子集上训练得到不同的决策树模型；

第三步，将训练得到的多个决策树模型进行组合，然后得到最后的输出结果。

如图1所示为随机对样本点和特征采样后训练得到的若干决策树模型组成的随机森林。从图中可以看出，即使同一个样本在不同树中所归属的叶子节点也不尽相同，甚至连类别也可能不同。但是这也充分体现了Bagging集成模型的优点，通过“平均”来提高模型的泛化能力。

在图1中，多个不同结构的决策树模型构成了随机森林，并且在模型输出时将会以投票的方式决策出最终的输出类别。同时，随机森林与普通Bagging集成学习方法存在的一点差别就是，随机森林中每一个决策树在每次划分节点的过程中，还会有一个随机的过程[2]，即只会从已有的特征中再随机选择部分特征参与节点划分，这一过程也被称为“Feature Bagging”。之所以要这么做是为了减小各个树模型之间的关联性。例如训练数据中存在着某些差异性较大的特征，那么所有的决策树在节点划分时就会选择同样的特征，使得最终得到的决策树之间具有较强的关联性，即每棵树都类似。

3.2 随机森林示例代码

介绍完随机森林的基本原理后，我们再来看一看如何通过sklearn完成随机森林的建模任务。在sklearn中，可以通过如下代码来导入模块随机森林。

xxxxxxxxxx
1
1
from sklearn.ensemble import RandomForestClassifier

下面先来介绍一下RandomForestClassifier类中常见的重要参数及其含义。

xxxxxxxxxx
9
1
1 def __init__(self,
2
2                  n_estimators=100,
3
3                  criterion="gini",
4
4                  max_depth=None,
5
5                  min_samples_split=2,
6
6                  min_samples_leaf=1,
7
7                  max_features="auto",
8
8                  bootstrap=True,
9
9                  max_samples=None):

上述代码是类RandomForestClassifier初始化方法中的部分参数，其中n_estimators表示在随机森林中决策树的数量；criterion表示指定构建决策树的算法；max_depth表示允许决策树的最大深度；min_samples_split表示节点允许继续划分的最少样本数，即如果划分后的节点中样本数少于该值，将不会进行划分；min_samples_leaf叶子节点所需要的最少样本数；max_features表示每次对节点进行划分时候选特征的最大数量，即节点每次在进行划分时会先在原始特征中随机的选取max_features个候选特征，然后在候选特征中选择最佳特征；bootstrap表示是否对原始数据集进行采样，如果为False则所有决策树在构造时均使用相同的样本;max_samples表示每个训练子集中样本数量的最大值（当bootstrap=True时），其默认值为None，即等于原始样本的数量。

注意：max_samples=None仅仅只是表示采样的样本数等于原始训练集的样本数，不代表抽样后的子训练等同于原始训练集，因为采样时样本可以重复。

一般来说，在sklearn的各个模型中，对于大多数参数来说保持默认即可，对于少部分关键参数可采样交叉验证进行选择。

下面以iris数据集为例来进行RandomForestClassifier的集成学习建模任务，完整代码见Chapter08/07_ensemble_random_forest.py文件。

xxxxxxxxxx
6
1
1 if __name__ == '__main__':
2
2     x_train, x_test, y_train, y_test = load_data()
3
3     model = RandomForestClassifier(n_estimators=2, max_features=3, 
4
4                                    random_state=2)
5
5     model.fit(x_train, y_train)
6
6     print(model.score(x_test, y_test)) # 0.95

可以看到，尽管随机森林这么复杂的一个模型，在sklearn中同样可以通过几行代码来完成建模。同时，在完成随机森林的训练后，可以通过model.estimators_属性来得到所有的决策树对象，然后分别对其进行可视化就可以得到整个随机森林可视化结果。当然，最重要的是可以通过model.feature_importances_属性来得到每个特征的重要性程度以进行特征筛选去掉无关特征。

3.3 特征重要性评估

从决策树的构造原理便可以看出，越是靠近决策树顶端的特征维度越能够对不同类别的样本进行区分，也就意味着越是接近于根节点的特征维度越重要。因此，在sklearn中的类DecisionTreeClassifier里面，同样也有feature_importances_属性来输出每个特征的重要性值。只是通过随机森林来进行特征重要性评估更加准确，因此掌柜才将这部分内容放到了这里。不过想要弄清楚随机森林中的特征重要性评估过程，还得从决策树说起。

1) 决策树中的特征评估

在sklearn中，决策树是通过基于基尼纯度的减少量来对特征进行重要性评估，当然基尼纯度也可以换成信息增益或者是信息增益比。具体的，对于决策树中划分每个节点的特征来说，其特征重要性计算公式为[2]

其中$N$$N$表 的样本数；$N_t$$N_t$表示当前节点的样本数；[impurity]表示当前节点的纯度； $N_{tL}$$N_{tL}$表示当前节点左孩子中的样本数；$\text{left\_impurity}$$\text{left\_impurity}$表示当前节点左孩子的纯度；$N_{tR}$$N_{tR}$表示当前节点右孩子中的样本数；$\text{right\_impurity}$$\text{right\_impurity}$表示当前节点右孩子的纯度。

以3.2小节随机森林里的其中一棵决策树为例，其在每次进行节点划分时的各项信息如图2所示。

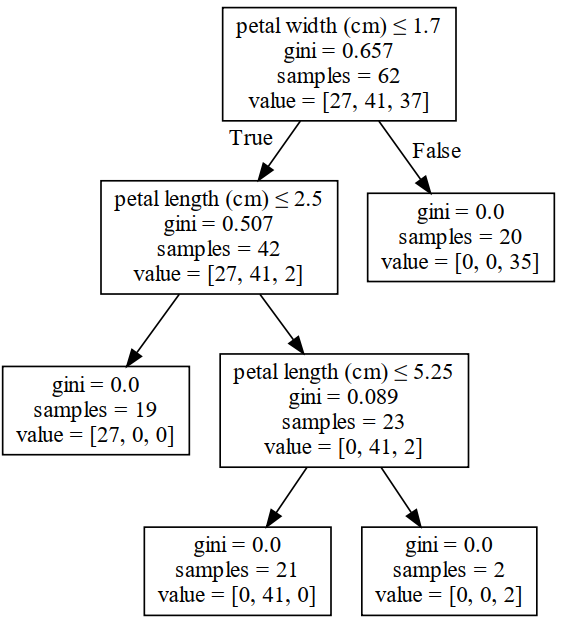
这里有一个小细节需要注意的地方便是，在图2中每个节点里samples的数量指的是不重复的样本数（因为采样会有重复），而列表value中的值则包含有重复样本。例如在根节点中，samples=62表示一共有62个不同的样本点，但实际上该节点中有105个样本点，即有43个重复出现。

此时，对于特征petal width来说，根据式$(2)$$(2)$其特征重要性值为

对于特征petal length来说，由于其在两次节点划分中均有参与，所以它的特征重要性为

对于另外两个特征sepal length和sepal width来说，由于两者并没有参与决策树节点的划分，所以其重要性均为0。

2) 随机森林中的特征评估

在介绍完决策树中的特征重要性评估后，再来看随机森林中的特征重要性评估过程就相对容易了。在sklearn中，随机森林的特征重要性评估主要也是基于多棵决策树的特征重要性结果计算而来，称为平均纯度减少量（Mean Decrease in Impurity,MDI）。MDI的主要计算过程就是将多棵决策树的特征重要性值取了一次平均。

对于3.2节中的随机森林来说，其另外一棵决策树在每次进行节点划分时的各项信息如图3所示。

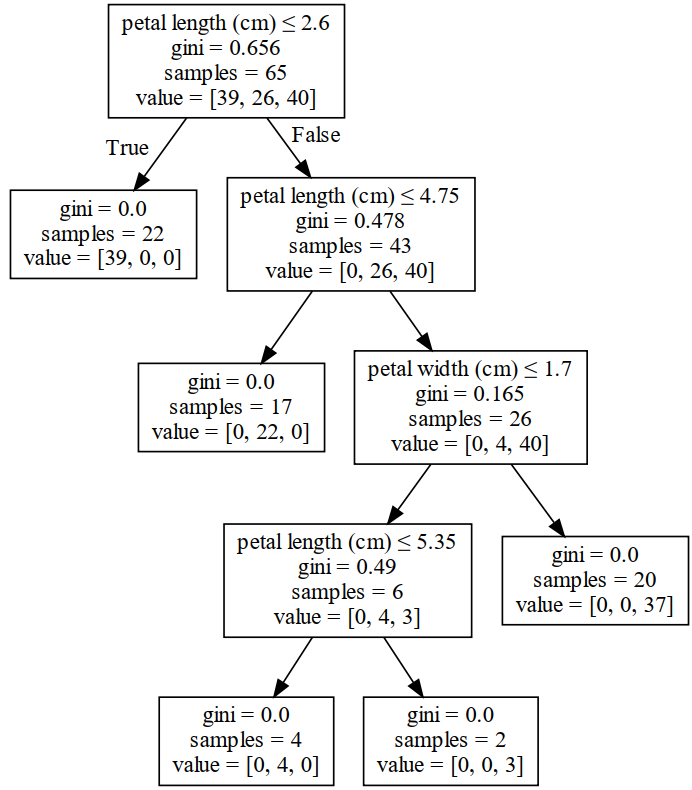
从图3可以看出，一共有2个特征参与到了节点的划分过程中。根据式$(2)$$(2)$可知，特征petal length的重要性为

特征petal width的重要性为

到此为止，对于3.2节中的随机森林，其两棵决策树对应的计算得到特征重要性如表2所示。

在sklearn中，对于决策树计算得到的特征重要性值默认情况下还会进行标准化，即每个维度均会除以所有维度的和。进一步，对于随机森林来说，其各个特征的重要性值则为所有决策树对应特征重要性的平均值。因此，对于表8-7中的结果来说最终每个特征重要性值为0，0，0.729和0.271。关于上述详细的计算过程可以参见Chapter08/08_ensemble_random_forest_features.py文件。

从最后的结果可以看出，在数据集iris中对分类起决定性作用的为最后两个特征维度。因此，各位读者也可以进行一个对比，只用最后两个维度来进行分类并观察其准确率。完整示例代码见Chapter08/09_feature_importance_comp.py文件。

4 泰坦尼克号预测

在本章的前面几节内容中，掌柜陆续介绍了几种决策树的生成算法以及常见的集成学习方法。在接下来的这节内容中，掌柜会将以泰坦尼克号生还预测（分类）[4] 为例来进行实战演示；并且还会介绍到相关的数据预处理方法，例如缺失值填充和类型特征转换等。

本次用到的数据集为泰坦尼克号生还预测数据集，原始数据集一共包含891个样本，11个特征维度。但是需要注意的是，在实际处理时这11个特征维度不一定都要用到，只选择你认为有用的即可。同时，由于部分样本存在某些特征维度出现缺失的状况，因此还需要对其进行填充。完整代码参见Chapter08/10_titanic.py文件。

4.1 读取数据集

本次用到的数据集一共包含两个文件，其中一个为训练集，另一个为测试集。下载完成后放在本代码所在目录的data目录中即可。接着可以通过如下代码来读入数据：

xxxxxxxxxx
4
1
1 import pandas as pd
2
2 def load_data():
3
3     train = pd.read_csv('data/train.csv',sep=’,’)
4
4     test = pd.read_csv('./data/test.csv')

在上述代码中，第1行用来导入库pandas用于读取本地文件；第3行代码表示通过pandas中的read_csv()方法来读取.csv文件，它返回的是一个DataFrame格式的数据类型，可以方便进行各类数据预处理操作。这里值得一提的是，read_csv不仅仅可以用来读取.csv格式的数据，只要读取的数据满足条件：①它是一个结构化的文本数据，即m行n列；②列与列之间有相同的分隔符，例如默认情况下sep=’,’。那么这样的数据都可以通过该方法来进行读取，不管文件的后缀是.csv还是.txt，亦或是没有后缀。当然，pandas还提供很多常见数据的读取方法，例如excel、json等。

在读取完成后，可以通过如下方式来查看数据集的相关信息：

xxxxxxxxxx
16
1
1 print(train.info())
2
 2 Data columns (total 12 columns):
3
 3  #   Column       Non-Null Count  Dtype  
4
 4 ---  ------       --------------  -----  
5
 5  0   PassengerId  891 non-null    int64  
6
 6  1   Survived     891 non-null    int64  
7
 7  2   Pclass       891 non-null    int64  
8
 8  3   Name         891 non-null    object 
9
 9  4   Sex          891 non-null    object 
10
10  5   Age          714 non-null    float64
11
11  6   SibSp        891 non-null    int64  
12
12  7   Parch        891 non-null    int64  
13
13  8   Ticket       891 non-null    object 
14
14  9   Fare         891 non-null    float64
15
15  10  Cabin        204 non-null    object 
16
16  11  Embarked     889 non-null    object

从上述输出信息可以知道，该数据集一共有11个特征维度（第1列Survived 为标签），891个样本。同时还可以具体的看到每个特征维度的数据类型、有少为非空值等信息。

4.2 特征选择

在完成原始数据的载入后，就需要对特征进行选择。对于特征的选择这一步显然是仁者见仁智者见智，可以都用上也可以只选择你认为对最后预测结果有影响的特征。在本示例中，掌柜选择的是'Pclass'、'Sex'、 'Age'、 'SibSp'、 'Parch'、'Fare'和'Embarked'这7个特征维度，其分别表示船舱等级、性别、年龄、乘客在船上兄弟姐妹/配偶的数量、乘客在船上父母/孩子的数量、船票费用和登船港口。当然， 'Survived'这一列特征是作为最终进行预测的类标。接着通过如下代码便可完成特征的选择工作：

xxxxxxxxxx
4
1
1 features = ['Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked']
2
2 x_train = train[features]
3
3 x_test = test[features]
4
4 y_train = train['Survived']

在上述代码中，第1行用来定义需要选择的特征；第2-3行用来在训练集和测试集中取对应的特征维度；第4行用来获取得到训练集中的标签。由于这是比赛中的数据集，所以真实的测试集中并不含有标签。

4.3 缺失值填充

在选择完成特征后下一步就是对其中的确实值进行填充。从上面的输出结果可以看出，在训练集和测试集中特征‘Age’、‘Embarked’和‘Fare’存在缺失值的情况。且特征‘Age’和‘Fare’均为浮点型，对于浮点型的缺失值一般可采用该特征维度所有值的平均作为填充；而特征‘Embarked’为类型值，对于类型值的缺失一般可以采用该特征维度出现次数最多的类型值进行填充。因此下面开始分别用这两种方法来进行缺失值的补充。

xxxxxxxxxx
5
1
1 x_train['Age'].fillna(x_train['Age'].mean(), inplace=True) 
2
2 print(x_train['Embarked'].value_counts())# S 644 C 168  Q 77
3
3 x_train['Embarked'].fillna('S', inplace=True)
4
4 x_test['Age'].fillna(x_train['Age'].mean(), inplace=True)
5
5 x_test['Fare'].fillna(x_train['Fare'].mean(), inplace=True)

在上述代码中，第1、4行用来对特征‘Age’以均值进行填充，这里需要注意的是测试集中的缺失值也应该用训练集中的均值来进行填充；第2行用来统计输出特征‘Embarked’中各个取值出现的次数，可以发现‘S’出现次数最多（644次）；第3行则用来对特征‘Embarked’的缺失值以‘S’进行填充。

4.4 特征值转换

在进行完上述几个步骤后，最后一步需要完成的就是对特征进行转换。所谓特征转换就是将其中的非数值型特征，用数值进行代替，例如特征‘Embarked’和‘Sex’。

xxxxxxxxxx
5
1
1 x_train.loc[x_train['Sex'] == 'male', 'Sex'] = 0
2
2 x_train.loc[x_train['Sex'] == 'female', 'Sex'] = 1
3
3 x_train.loc[x_train['Embarked'] == 'S', 'Embarked'] = 0
4
4 x_train.loc[x_train['Embarked'] == 'C', 'Embarked'] = 1
5
5 x_train.loc[x_train['Embarked'] == 'Q', 'Embarked'] = 2

在上述代码中，.loc方法用来获取对应行列索引中的值，而类似x_train['Sex'] == 'male'则是用来得到满足条件的行索引。经过上述步骤后，数据集中的字符特征就被替换成了对应的数值特征。

4.5 乘客生还预测

在完成数据预处理的所有工作后，便可以建立相应的分类模型来对测试集中的乘客生还情况进行预测。下面以随机森林模型进行示例。

xxxxxxxxxx
11
1
1 def random_forest():
2
 2     x_train, y_train, x_test = load_data()
3
 3     model = RandomForestClassifier()
4
 4     paras = {'n_estimators': np.arange(10, 100, 10), 
5
 5              'criterion': ['gini', 'entropy'], 
6
 6              'max_depth': np.arange(5, 50, 5)}
7
 7     gs = GridSearchCV(model, paras, cv=5, verbose=2, n_jobs=2)
8
 8     gs.fit(x_train, y_train)
9
 9     y_pre = gs.predict(x_test)
10
10     print('best score:', gs.best_score_) # 0.827
11
11     print('best parameters:', gs.best_params_)

由于上述示例代码在3.2节中均有介绍，所以在此就不再赘述。

5 总结

总结一下，在这篇文章中掌柜首先介绍了集成学习算法的基本思想，并就3种常见的集成学习算法Bagging、Boosting和Stacking进行了简单的介绍和示例；然后详细介绍了随机森林以及特征重要性的计算原理；最后，掌柜通过一个真实的比赛数据集，详细介绍了从数据预处理到模型训练与预测的全过程。经过以上内容的学习，会使得我们对于如何从零构建一个机器学习模型有了更深的理解。

本次内容就到此结束，感谢您的阅读！如果你觉得上述内容对你有所帮助，欢迎点赞分享！若有任何疑问与建议，请添加掌柜微信nulls8（备注来源）或加群进行交流。青山不改，绿水长流，我们月来客栈见！

引用

[1] https://en.wikipedia.org/wiki/Ensemble_learning

[2] Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825-2830, 2011.

[3] https://en.wikipedia.org/wiki/Random_forest

[4] https://www.kaggle.com/c/titanic/data

推荐阅读

[1] 决策树之ID3和C4.5原理与实战

[2] CART生成与剪枝算法