决策树之ID3和C4.5原理与实战

各位客官大家好，欢迎来到月来客栈，我是掌柜空字符。

经过前面几个章节的介绍，我们已经学习过了3个分类算法模型，包括逻辑回归、K近邻和朴素贝叶斯。今天掌柜将开始介绍下一个分类算法模型决策树（Decision Tree）。

1 决策树的基本思想

一说到决策树其实很读者或多或少都已经使用过，只是自己还不知道罢了。例如最简单的决策树就是通过输入年龄，判读其是否为成年人，即if age >= 18 return True，想想自己是不是经常用到这样的语句?

1.1 冠军球队

关于什么是决策树，我们先来看这么一个例子。假如掌柜错过了某次世界杯比赛，赛后掌柜问一个知道比赛结果的人“哪支球队是冠军”？但是对方并不愿意直接说出结果，而是让掌柜自己猜，且每猜一次对方都要收一元钱才肯告诉掌柜是否猜对了。那现在的问题是要掏多少钱才能知道谁是冠军球队呢[1]？

现在我可以把球队从1到16编上号，然后提问：“冠军球队在1-8号中吗？”。假如对方告诉我猜对了，掌柜就会接着问：“冠军在1-4号中吗？”。假如对方告诉我猜错了，那么掌柜也就自然知道冠军在5-8号中。这样只需要4次，掌柜就能知道哪支球队是冠军。上述过程背后所隐藏着的其实就是决策树的基本思想，并且还可以用更为直观的图来展示上述的过程，如图8-1所示。

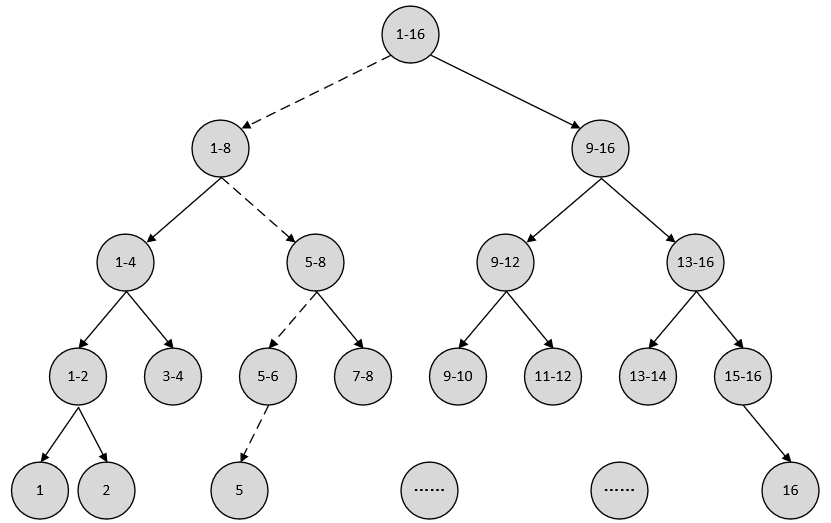
由此可以得出，决策树每一步的决策过程就是降低信息不确定性的过程，甚至还可以将这些决策看成是一个if-then的规则集合。如图8-1所示，冠军球队一开始有16种可能性，经过一次决策后变成了8种。这意味着每次决策都能得到更多确定的信息，而减少更多的不确定性。

不过现在的问题是，为什么要像图8-1这样来划分球队？对于熟悉足球的读者来说，这样的决策树似乎略显多余。因为事实上只有少数几支球队才有夺冠的希望，而大多数是没有的。因此，一种改进做法就是在一开始的时候就将几个热门的可能夺冠的球队分在一边，将剩余的放在另一边，这样就可以大大提高整个决策过程的效率。

例如最有可能夺冠的是1,2,3,4这4个球队，而其余球队夺冠的可能性远远小于这4个。那么一开始就可以将球队分成1-4和5-16。如果冠军是在1-4中，那么后面很快就能知道谁是冠军。退一万步，假如冠军真的是在5-16，那么接下来你同样可以按照类似的思路将剩余的球队划分成最有可能夺冠和最不可能夺冠这两个部分。这样也能快速的找出谁是冠军球队。

于是这时候可以发现，如何划分球队变成了建立这棵决策树的关键。如果存在一种划分，能够使得数据的“不确定性”减少得越多（谁不可能夺冠），也就意味着该划分能获取更多的信息，而我们也就更倾向于采取这样的划分。因此采用不同的划分就会得到不同的决策树。所以，现在的问题就变成了如何构建一棵“好”的决策树呢？要想回答这个问题，先来解决如何描述“信息”这个问题。

1.2 信息的度量

关于如何定量的来描述信息，几千年来都没有人给出很好的解答。直到1948年，香农在他著名的论文“通信的数学原理”中提出了信息熵（Information Entropy）的概念，这才解决了信息的度量问题，并且还量化出了信息的作用。

1) 信息熵

一条信息的信息量与其不确定性有着直接的关系。比如说，要搞清楚一件非常非常不确定的事，就需要了解大量的信息。相反，如果已经对某件事了解较多，则不需要太多的信息就能把它搞清楚。所以从这个角度来看可以认为，信息量就等于不确定性的多少。我们经常说，一句话包含有多少信息，其实就是指它不确定性的多与少。

于是，8.1.1节中第一种划分方式的不确定性（信息量）就等于“4块钱”，因为掌柜花4块钱就可以解决这个不确定性。当然，香农用的不是钱，而是用“比特”（Bit）这个概念来度量信息量，一个字节就是8比特。在上面的第一种情况中，“谁是冠军”这条消息的信息量就是4比特。那4比特是怎么计算来的呢？第二种情况的信息量又是多少呢？

香农指出，它的准确信息量应该是

其中$\log$$\log$表示以2为底的对数，$p_1,p_2,...,p_{16}$$p_1,p_2,...,p_{16}$分别是这16支球队夺冠的概率。香农把式$(8.1)$$(8.1)$的结果称为“信息熵（Entropy），一般用符号$\mathrm{H}$$\mathrm{H}$表示，单位是比特。由于在第一种情况中，默认条件是16支球队夺冠概率相同，因此对应的信息熵就是4比特。

对于任意一个随机变量$X$$X$（比如得冠军的球队），它的熵定义如下[2]

其中$\log$$\log$表示以2为底的对数 。

例如在二分类问题中：设$P(y=0)=p,P(y=1)=1-p,0\le p\le 1$$P(y=0)=p,P(y=1)=1-p,\;0\leq p\leq1$，那么此时的信息熵$H(y)$$H(y)$即为：

根据式还$(8.3)$$(8.3)$能画出其对应的函数图像，如图8-2所示。

从图8-2可以发现，当两种情况发生的概率均等（$p=1-p=0.5$$p=1-p=0.5$）时信息熵最大，也就是说此时的不确定性最大，要把这件事搞清楚所需要的信息量也就越大。并且这也很符合我们的常识，例如“明天下雨和不下雨的概率都是50%”，那么这一描述所存在的不确定性是最大的。

2) 条件熵

在谈条件熵（Condition Entropy）之前，我们先来看看信息的作用。一个事物（那只球队会得冠），其内部会存有随机性也就是不确定性，假定其为$U$$U$。从外部消除这个不确定性的唯一办法就是引入信息$I$$I$（我来猜，另一个人给我反馈）。并且需要引入的信息量取决于这个不确定性的大小，即$I>U$$I>U$才能完全消除这一不确定性。当$I<U$$I<U$时，外部信息可以消除一部分不确定性，也就是说新的不确定性$U^{\prime }=U-I$$U^{\prime}=U-I$。反之，如果没有信息的引入，那么任何人都无法消除原有的不确定性[1]。而所谓条件熵，说得简单点就是在给定某种条件（有用信息）$I$$I$下，事物$U$$U$的熵，即$H(U|I)$$H(U|I)$。

到此，对于条件熵相信读者朋友们在感性上已经有了一定的认识。至于具体的数学定义将在决策树生成部分进行介绍。

3) 信息增益

在8.1.1节中掌柜介绍到，若一种划分能使数据的“不确定性”减少得越多，也就意味着该种划分能获取更多的信息，而我们也就更倾向于采取这样的划分。也是就说，存在某个事物$I$$I$，当引入事物$I$$I$的信息后$U$$U$的熵变小了。而我们要选的就是那个最能使得$U$$U$的信息熵变小的$I$$I$，即需要得到最大的信息增益（Information Gain）

综上所述，采用不同的划分就会得到不同的决策树，而我们所希望得到的就是在每一次划分的时候都采取最优的方式，即局部最优解。这样每一步划分都能够使得当前的信息增益达到最大。因此可以得出，构建决策树的核心思想就是每次划分时，要选择使得信息增益达到最大时的划分方式，以此来递归构建决策树。

1.3 小结

在本节中，掌柜首先介绍了决策树的核心思想，即决策树的本质就是降低信息不确定性的过程；然后总结出构建一棵决策树的关键在于找到一种合适的划分，使得信息的“不确定性”能够降低得最多；最后掌柜介绍了如何以量化的方式来对信息进行度量。

2 决策树的生成之ID3与C4.5

在正式介绍决策树的生成算法前，掌柜先将8.1.1节中介绍的几个概念重新梳理一下；并且同时再通过一个例子来熟悉一下计算过程，以便于后续更好的理解决策树的生成算法。

2.1 基本概念与定义

1) 信息熵

设$X$$X$是一个取值有限的离散型随机变量（例如上一小节中可能夺冠的16只球队），其概率分布为$P(X=x_i)=p_i,i=1,2,...,n$$P(X=x_i)=p_i,\;i=1,2,...,n$（每个球队可能夺冠的概率），则随机变量$X$$X$的信息熵定义为

其中，若$p_i=0$$p_i=0$，则定义$0\log 0=0$$0\log0=0$；且通常$\log$$\log$取2为底或$e$$e$为底时，其熵的单位分别称为比特（Bit）或纳特（Nat）。如无特殊说明，默认以2为底。

2) 条件熵

设有随机变量$(X,Y)$$(X,Y)$，其联合概率分布分$P(X=x_i,Y=y_i)=p_{ij}$$P(X={{x}_{i}},Y={{y}_{i}})={{p}_{ij}}$，其中$i=1,2,...,n$$\ i=1,2,...,n$，$P(X=x_i,Y=y_i)=p_{ij},$$P(X=x_i,Y=y_i)=p_{ij},$ $i=1,2,...,n;$$i=1,2,...,n;$$j=1,2,...,m$$j=1,2,...,m$；条件熵$H(Y|X)$$H(Y|X)$表示在已知随机变量$X$$X$的条件下，随机变量$Y$$Y$的不确定性，其定义为

其中，$p_i=P(X=x_i),i=1,2,...,n$$p_i=P(X=x_i),i=1,2,...,n$

同时，当信息熵和条件熵中的概率由样本数据估计（特别是极大似然估计）得到时，所对应的信息熵与条件熵分别称之为经验熵（Empirical Entropy）和经验条件熵（Empirical Conditional Entropy）。这里暂时看不懂没关系，请结合后续计算示例。

3) 信息增益

从8.1.1节的内容可知，所谓信息增益指的就是事物$U$$U$的信息熵$H(U)$$H(U)$，在引入外部信息$I$$I$后的变化量$H(U)-H(U|I)$$H(U)-H(U|I)$。因此，可以将特征$A$$A$对训练数据集$D$$D$的信息增益$d(D,A)$$d(D,A)$定义为集合$D$$D$信息熵$H(D)$$H(D)$与特征$A$$A$给定条件下$D$$D$的条件熵$H(D|A)$$H(D|A)$之差，即

定义：设训练集为$D$$D$，$\left|D\right|$$\left| D \right|$表示所有训练样本总数；同时$D$$D$有$K$$K$个类别$C_k,k=1,2,...,K;|C_k|$$C_k,k=1,2,...,K;\;|C_k|$为属于类$C_k$$C_k$的样本总数，即${\sum }_{k=1}^K|C_k|=|D|$$\sum\nolimits_{k=1}^{K}{|{{C}_{k}}|}=|D|$；设特征$A$$A$有$n$$n$个不同的取值$a_1,a_2,...,a_n$${a_1,a_2,...,a_n}$，根据特征$A$$A$的取值将$D$$D$划分为$n$$n$个子集$D_1,D_2,...,D_n$$D_1,D_2,...,D_n$，$|D_i|$$|D_i|$为子集$D_i$$D_i$中的样本个数，即${\sum }_{i=1}^n|D_i|=|D|$$\sum\nolimits_{i=1}^{n}{|{{D}_{i}}|=|D|}$；同时记子集$D_i$$D_i$中，属于类$C_k$$C_k$的样本集合为$D_{ik}$$D_{ik}$，即$D_{ik}=D_i\bigcap C_k$${{D}_{ik}}={{D}_{i}}\bigcap {{C}_{k}}$，$|D_{ik}|$$|D_{ik}|$为$D_{ik}$$D_{ik}$的样本个数。此时如下定义[2]

• 数据集$D$$D$的经验熵$H(D)$$H(D)$为

  $$H(D)=-\sum _{k=1}^K\frac{|C_k|}{|D|}{\log }_2\frac{|C_k|}{|D|}(8.8)$$

  从式$(8.8)$$(8.8)$可以看出，它计算的是“任意样本属于其中一个类别”这句话所包含的信息量。

• 数据集$D$$D$在特征值$A$$A$下的经验条件熵$H(D|A)$$H(D|A)$为

  $$H(D|A)=\sum _{i=1}^n\frac{|D_i|}{|D|}H(D_i)=-\sum _{i=1}^n\frac{|D_i|}{|D|}\sum _{k=1}^K\frac{|D_{ik}|}{|D_i|}{\log }_2\frac{|D_{ik}|}{|D_i|}(8.9)$$

  从式$(8.9)$$(8.9)$可以看出，它计算的是特征$A$$A$在各个取值条件下“任意样本属于其中一个类别”这句话所包含的信息量。

• 信息增益为

  $$g(D,A)=H(D)-H(D|A)(8.10)$$

2.2 计算示例

如果仅看上面的公式肯定会不那么容易理解，下面掌柜再进行举例说明（将上面的公式同下面的计算过程对比看会更容易理解）。下表8-1同样是6.1.3节中用过的一个信用卡审批数据集，其一共包含15个样本和3个特征维度。其中特征$X^{(1)}\in A_1=\{0,1\}$$X^{(1)}\in A_1=\{0,1\}$表示有无工作，特征$X^{(2)}\in A_2=\{0,1\}$$X^{(2)}\in A_2=\{0,1\}$表示是否有房，特征$X^{(3)}\in A_3=\{D,S,T\}$${{X}^{(3)}}\in {{A}_{3}}=\{D,S,T\}$表示学历等级，$Y\in C=\{0,1\}$$Y\in C=\{0,1\}$表示是否审批通过的类标记。

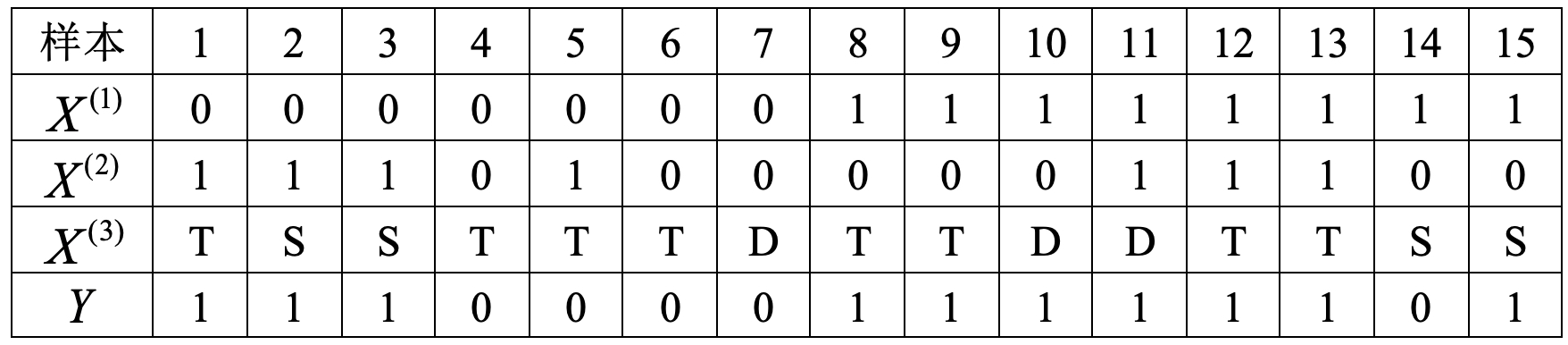
1) 计算信息熵

根据式$(8.8)$$(8.8)$可得

2) 计算条件熵

由表8-1可知，数据集有3个特征（工作、房子、学历）$A_1,A_2,A_3$$A_1,A_2,A_3$；接下来根据式来计算$D$$D$分别在3个特征取值条件下的条件熵$H(D|A_i)$$H(D|A_i)$。

• 已知外部信息“工作”的情况下有

  $$\begin{array}{rl}& H(D|A_1)=[\frac{7}{15}H(D_1)+\frac{8}{15}H(D_2)]\\ & =-\frac{7}{15}(\frac{3}{7}{\log }_2\frac{3}{7}+\frac{4}{7}{\log }_2\frac{4}{7})-\frac{8}{15}(\frac{7}{8}{\log }_2\frac{7}{8}+\frac{1}{8}{\log }_2\frac{1}{8})\approx 0.75\end{array}(8.12)$$

  式$(8.12)$$(8.12)$中，$D_1,D_2$$D_1,D_2$分别是$A_1$$A_1$取值为“无工作”和“有工作”时，训练样本划分后对应的子集。

• 已知外部信息“房子”的情况下有

  $$\begin{array}{rl}& H(D|A_2)=[\frac{8}{15}H(D_1)+\frac{7}{15}H(D_2)]\\ & =-\frac{8}{15}(\frac{4}{8}{\log }_2\frac{4}{8}+\frac{4}{8}{\log }_2\frac{4}{8})-\frac{7}{15}(\frac{1}{7}{\log }_2\frac{1}{7}+\frac{6}{7}{\log }_2\frac{6}{7})\approx 0.81\end{array}(8.13)$$

  式$(8,13)$$(8,13)$中，$D_1,D_2$$D_1,D_2$分别是$A_2$$A_2$取值为“无房”和“有房”时，训练样本划分后对应的子集。

• 已知外部信息“学历”的情况下有

  $$\begin{array}{rl}& H(D|A_3)=[\frac{3}{15}H(D_1)+\frac{4}{15}H(D_2)+\frac{8}{15}H(D_3)]\\ & =-\frac{3}{15}(\frac{1}{3}{\log }_2\frac{1}{3}+\frac{2}{3}{\log }_2\frac{2}{3})-\frac{4}{15}(\frac{1}{4}{\log }_2\frac{1}{4}+\frac{3}{4}{\log }_2\frac{3}{4})\\ & -\frac{8}{15}(\frac{3}{8}{\log }_2\frac{3}{8}+\frac{5}{8}{\log }_2\frac{5}{8})\approx 0.91\end{array}(8.14)$$

  式$(8.14)$$(8.14)$中，$D_1,D_2,D_3$${{D}_{1}},{{D}_{2}},{{D}_{3}}$分别是$A_3$${{A}_{3}}$取值为“D”、“S”和“T”时，训练样本划分后对应的子集。

3) 计算信息增益

根据上面的计算结果便可以计算得到各特征划分下的信息增益为

到目前为止，我们已经知道了在生成决策树的过程中所需要计算的关键步骤信息增益，接下来，掌柜就开始正式介绍如何生成一棵决策树。

2.3 ID3生成算法

在8.1节的末尾掌柜总结到，构建决策树的核心思想就是：每次划分时，要选择使得信息增益最大的划分方式，以此来递归构建决策树。如果利用一个特征进行分类的结果与随机分类的结果没有很大差别，则称这个特征没有分类能力。因此，对于决策树生成的一个关键步骤就是选取对训练数据具有分类能力的特征，这样可以提高决策树学习的效率，而通常对于特征选择的准则就是8.1节谈到的信息增益。

ID3（Interactive Dichotomizer-3）算法的核心思想是在选择决策树的各个节点时，采用信息增益来作为特征选择的标准，从而递归地构建决策树。其过程可以概括为，从根节点开始计算所有可能划分情况下的信息增益；然后选择信息增益最大的特征作为划分特征，由该特征的不同取值建立子节点；最后对子节点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有可以选择为止。例如根据8.2.2节最后的计算结果可知，首先应该将数据样本以特征$A_1$$A_1$有无工作）作为划分方式对数据集进行第一次划分。下面开始介绍通过ID3来生成决策树的步骤及示例。

• 生成步骤

  输入：训练数据集$D$$D$，特征集$A$$A$，阈值$\epsilon$$\varepsilon$;

  输出：决策树[2]。

  (1) 若$D$$D$中所有样本属于同一类$C_k$$C_k$（即此时只有一个类别）则T为单节点树，将$C_k$$C_k$作为该节点的类标记，返回T;

  (2) 若$A=\mathrm{\varnothing }$$A=\emptyset$，则T为单节点树，并将$D$$D$中样本数最多的类$C_k$$C_k$作为该节点的类标记，并返回T；

  (3) 否则，计算$A$$A$中各特征对$D$$D$的信息增益，选择信息增益最大的特征$A_g$$A_g$；

  (4) 如果$A_g$$A_g$的信息增益小于阈值$\epsilon$$\varepsilon$，则置T为单节点树，并将$D$$D$中样本数最多的类$C_k$$C_k$作为该节点的类标记，返回T；

  (5) 否则，对$A_g$$A_g$的每一个可能值$a_i$$a_i$，以$A_g=a_i$$A_g=a_i$将$D$$D$分割为若干非空子集，并建立为子节点；

  (6) 对于第$i$$i$个子节点，以$D_i$$D_i$为训练集，以$A-\{A_g\}$$A-\{A_g\}$为特征集，递归地调用(1)-(5)，得到子树$T_i$$T_i$，返回$T_i$$T_i$。

• 生成示例

  下面就用ID3算法来对表8-1中的数据样本进行决策树生成示例。易知该数据集不满足步骤(1)(2)中的条件，所以开始执行步骤(3)。同时，根据8.2.2小节最后的计算结果可知，对于特征$A_1,A_2,A_3$$A_1,A_2,A_3$来说，在$A_1$$A_1$条件下信息增益最大，所以应该选择特征$A_1$$A_1$作为决策树的根节点。

  由于本例中未设置阈值，所以接着执行步骤(5)按照$A_1$$A_1$的取值将训练集$D$$D$划分为两个子集$D_1,D_2$$D_1,D_2$，如表8-2所示。

  表8-2 第一次划分表

  

  接着开始执行步骤(6)，由于$D_1,D_2$$D_1,D_2$均不满足步骤(1)(2)中的条件，所以两部分需要分别继续执行后续步骤，此时生成的决策树如图8-3所示。

  

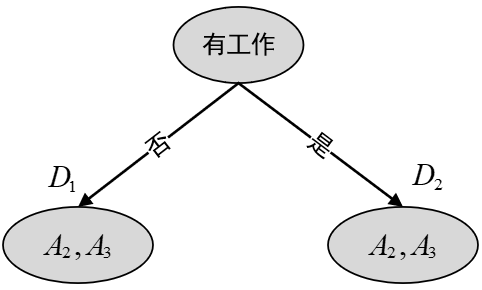
  图8-3 第一次划分

  此时，对于子集$D_1$$D_1$来说，需要从特征$A-\{A_g\}$$A-\{A_g\}$中即$A_2,A_3$$A_2,A_3$中选择新的特征，并计算信息增益。

  1) 计算信息熵$H(D_1)$$H(D_1)$

  $$H(D_1)=-(\frac{3}{7}{\log }_2\frac{3}{7}+\frac{4}{7}{\log }_2\frac{4}{7})\approx 0.985(8.16)$$

  2) 计算条件熵

  $$H(D_1|A_2)=-\frac{3}{7}(\frac{3}{3}{\log }_2\frac{3}{3}+0)-\frac{4}{7}(\frac{1}{4}{\log }_2\frac{1}{4}+\frac{3}{4}{\log }_2\frac{3}{4})\approx 0.464(8.17)$$
  $$H(D_1|A_3)=-\frac{1}{7}(0+0)-\frac{2}{7}(0+0)-\frac{4}{7}(\frac{3}{4}{\log }_2\frac{3}{4}+\frac{1}{4}{\log }_2\frac{1}{4})\approx 0.464(8.18)$$

  根据式$(8.17)$$(8.17)$和$(8.18)$$(8.18)$的结果可知，对于子集$D_1$$D_1$来说，无论其采用$A_2,A_3$$A_2,A_3$中的哪一个特征进行划分，最后计算得到的信息增益都是相等的，所以这里不妨就以特征$A_2$$A_2$进行划分。

  同理，对于子集$D_2$${{D}_{2}}$来说，也需要从特征$A-\{A_g\}$$A-\{A_g\}$中即$A_2,A_3$$A_2,A_3$中选择新的特征，并计算信息增益。

  1) 计算信息熵

  $$H(D_2)=-(\frac{1}{8}{\log }_2\frac{1}{8}+\frac{7}{8}{\log }_2\frac{7}{8})\approx 0.544(8.19)$$

  2) 计算条件熵

  $$H(D_2|A_2)=-\frac{5}{8}(\frac{1}{5}{\log }_2\frac{1}{5}+\frac{4}{5}{\log }_2\frac{4}{5})-\frac{3}{8}(0+0)\approx 0.451(8.20)$$
  $$H(D_2|A_3)=-\frac{2}{8}(0+0)-\frac{2}{8}(\frac{1}{2}{\log }_2\frac{1}{2}+\frac{1}{2}{\log }_2\frac{1}{2})-\frac{4}{8}(0+0)=0.25(8.21)$$

  3) 信息增益

  $$\begin{array}{rl}& g(D_2|A_2)=0.544-0.451=0.093\\ & g(D_2|A_3)=0.544-0.25=0.294\end{array}(8.22)$$

  根据式$(8.22)$$(8.22)$的计算结果可知，对于子集$D_2$$D_2$来说，采用特征$A_3$$A_3$来对其进行划分时所产生的信息增益最大，因此应该选择特征$A_3$$A_3$来作为子集$D_2$${{D}_{2}}$的根节点。

  到此，根据上述计算过程，便可以得到第二次划分后的结果，如表8-3所示。

  表8-3 第二次划分表

  

  从表8-3中的结果可知，$D_{11},D_{21},D_{23}$$D_{11},D_{21},D_{23}$这三个子集中样本均只有一个类别，既满足生成步骤中的第(1)步，故此时可以得到第二次划分后的决策树，如图8-4所示。

  

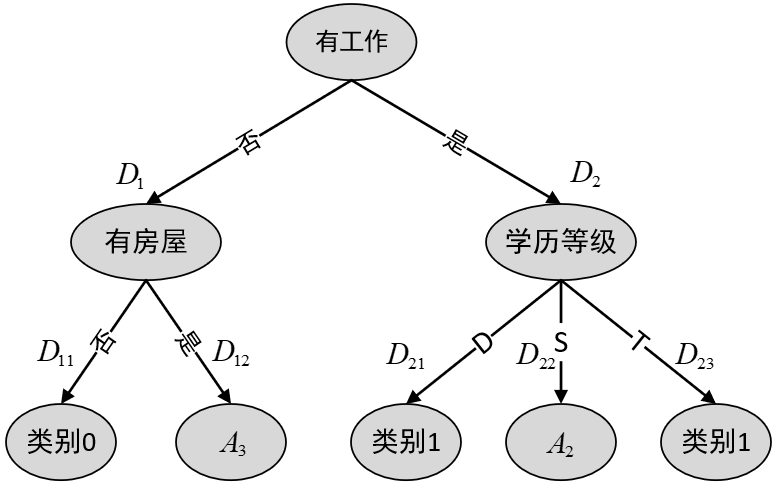
  图8-4 第二次划分

  由于子集$D_{12},D_{22}$$D_{12},D_{22}$均不满足终止条件(2)(4)，且此时两个子集中均只有一个特征可以选择，所以并不需要再进行比较直接划分即可得，如表8-4所示。

  表8-4 第三次划分表

  

  根据表8-4中的结果可知，子集$D_{121}$$D_{121}$满足生成步骤中的第(1)步，故此时可以得到第三次划分后的决策树，如图8-5所示。

  

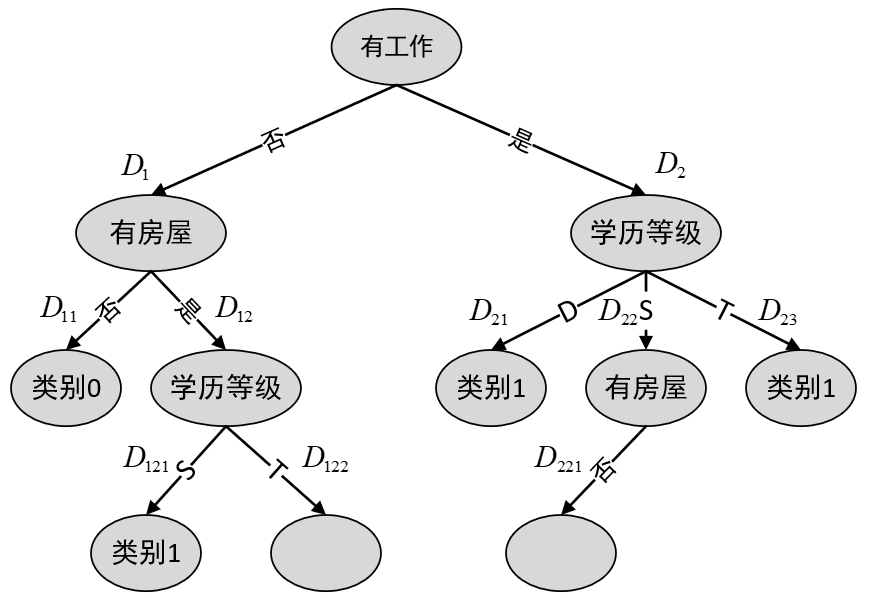
  图8-5 第三次划分

  此时，由于子集$D_{122},D_{221}$$D_{122},D_{221}$满足生成步骤中第 (2)步的终止条件，即再无特征可以进行划分，需要选择样本数最多的类别作为该节点的类别进行返回。但巧合的是子集$D_{122},D_{221}$$D_{122},D_{221}$中不同类别均只有一个样本，因此随机选择一个类别即可。不过在实际过程中很少会出现这样的情况，因为一般当节点的样本数小于某个阈值时也会停止继续划分。这样便能得到最终生成的决策树，如图8-6所示。

  

如上就是通过ID3算法生成整个决策树的详细过程。根据生成步骤可以发现，如果单纯以$g(D,A)$$g(D,A)$作为标准的话，会存在模型倾向于选择取值较多的特征进行划分（比如上面的$A_2$$A_2$）。虽然在上面这个例子中不存在，但是我们仍可以从直观上理解为什么ID3会倾向于选取特征值取值较多的特征。由于$g(D,A)$$g(D,A)$的直观意义是$D$$D$被$A$$A$划分后不确定性的减少量，因此可想而知当$A$$A$的取值情况越多，那么$D$$D$会被划分得到的子集就越多，于是其不确定性自然会减少得越多，从而ID3算法会倾向于选择取值较多的特征进行划分。可以想象，在这样的情况下最终得到的决策树将会是一颗很胖很矮的决策树，进而导致最后生成的决策树容易出现过拟合现象。

2.4 C4.5生成算法

为了解决ID3算法的弊端，进而产生了C4.5算法。C4.5算法与ID3算法相似，不同之处仅在于C4.5算法在选择特征的时候采用了信息增益比作为标准，即选择信息增益比最大的特征作为当前样本集合的根节点。具体为，特征$A$$A$对训练集$D$$D$的信息增益比$g_R(D,A)$$g_R(D,A)$定义为其信息增益$g(D,A)$$g(D,A)$与其训练集$D$$D$关于特征$A$$A$的信息熵$H_A(D)$$H_A(D)$之比，即

其中，$H_A(D)=-{\displaystyle \sum _{i=1}^n\frac{|D_i|}{|D|}{\log }_2\frac{|D_i|}{|D|}}$$H_A(D)=-\displaystyle\sum_{i=1}^n\frac{|D_i|}{|D|}\log_2{\frac{|D_i|}{|D|}}$，$n$$n$是特征$A$$A$取值的个数。

因此，8.2.3节的例子中，对于选取根节点时其增益比计算如下：

1. 计算得到信息增益

2. 计算各特征的信息熵

3. 计算信息增益比

根据式$(8.26)$$(8.26)$的计算结果，此时应该以特征$A_1$$A_1$的各个取值对样本集合$D$$D$进行划分。

由此，可以将利用C4.5算法来生成决策树的过程总结如下：

输入：训练数据集D，特征集A，阈值$\epsilon$$\varepsilon$;

输出：决策树。

(1) 若$D$$D$中所有样本属于同一类$C_k$$C_k$，则T为单节点树，并将$C_k$$C_k$作为该节点的类标记，返回T;

(2) 若$A=\mathrm{\varnothing }$$A=\emptyset$，则T为单节点树，并将$D$$D$中样本数最多的类$C_k$$C_k$作为该 节点的类标记，返回T；

(3) 否则，计算$A$$A$中各特征对$D$$D$的信息增益比，选择信息增益比最大的特征$A_g$$A_g$；

(4) 如果$A_g$$A_g$的信息增益比小于阈值$\epsilon$$\varepsilon$，则置T为单节点树，并将$D$$D$中样本数最多的类$C_k$$C_k$作为该节点的类标记，返回T；

(5) 否则，对$A_g$$A_g$的每一个可能值$a_i$$a_i$，以$A_g=a_i$$A_g=a_i$将D分割为若干非空子集，并建立为子节点；

(6) 对于第$i$$i$个子节点，以$D_i$$D_i$为训练集，以$A-\{A_g\}$$A-\{A_g\}$为特征集，递归地调用(1)-(5)，得到子树$T_i$$T_i$，并返回$T_i$$T_i$

从以上生成步骤可以看出，C4.5算法与ID3算法的唯一为别就是选择的标准不同，而其它的步骤均一样。到此为止，我们就学习完了决策树中的ID3与C4.5生成算法。在8.3节中，将来通过sklearn来完成决策树的建模工作。

2.5 特征划分

在经过上述两个小节的介绍之后，相信读者朋友们对于如何通过ID3和C4.5算法来构造一棵简单的决策树已经有了基本的了解。不过细心的读者可能会有这样一个疑问，那就是如何来处理连续型的特征变量。

从上面的示例数据集可以看出，工作、房子、学历这三个都属于离散型的特征变量（Discrete Variable），即每个特征的取值都属于某一个类别；而通常在实际建模过程中，更多的会是连续型的特征变量（Continuous Variable），例如年龄、身高等。在sklearn所实现的决策树算法中，对于这种连续型的特征变量，其具体做法便是先对其进行排序处理，然后取所有连续两个值的均值来离散化整个连续型特征变量[3]。

假设现在某数据集其中一个特征维度为

则首先需要对其进行排序处理，排序后的结果为

接着再计算所有连续两个值之间的平均值

这样，便得到了该特征离散化后结果。最后在构造决策树时，只需要使用式$(8.29)$$(8.29)$中离散化后的特征进行划分指标的计算即可。同时，值得一说的地方是目前sklearn在实际处理时，把所有的特征均看作连续型变量在进行处理。

2.6 小结

在本节中，掌柜首先回顾了决策树中几个重要的基本概念，并同时进行了相关示例计算；接着介绍了如何通过信息增益这一划分标准（即ID3算法）来构造生成决策树，并以一个真实的例子进行了计算示例；然后，介绍了通过引入信息增益比（即C4.5算法）这一划分标准来解决ID3算法在生成决策树时所存在的弊端；最后，介绍了在决策树生成时，如何处理连续型特征变量的一种常用方法。

3 决策树生成与可视化

在清楚决策树的相关生成算法后，再利用sklearn建模就变得十分容易了。下面使用的依旧是前面介绍的iris数据集，完整代码见Book\Chapter08\01_decision_tree_ID3.py文件。

3.1 ID3算法示例代码

在正式建模之前，掌柜先来对sklearn中类DecisionTreeClassifier里的几个常用参数进行简单的介绍。

xxxxxxxxxx
8
1
1 def __init__(self, *,
2
2     criterion="gini",
3
3     splitter="best",
4
4     max_depth=None,
5
5     min_samples_split=2,
6
6     min_samples_leaf=1,
7
7     max_features=None,
8
8     min_impurity_split=None): 

在上述代码中，criterion用来选择划分时的度量标准，当criterion="entropy"时表示使用信息增益作为划分指标；splitter用来选择节点划分时的特征选择策略，当splitter="best"时则每次节点进行划分时均在所有特征中通过度量标准来选择最优划分方式，而当splitter="random"时则每次节点进行划分时只会随机选择max_features个特征，并在其中选择最优划分方式；max_depth表示决策树的最大深度，默认为None表示直到所有叶子节点的样本均为同一类别或者是样本数小于min_samples_split时停止划分；min_samples_leaf指定构成一个叶子节点所需要的最少样本数，即如果划分后叶子节点中的样本数小于该阈值，则不会进行划分；min_impurity_split用来提前停止节点划分的阈值，默认为None即无阈值。

1) 载入数据集

在介绍完类DecisionTreeClassifier的基本用法后，便可以通过其来完成决策树的生成。首先需要载入训练模型时所用到的数据集，同时为了后续更好的观察可视化后的决策树，所以这里也要返回各个特征的名称，代码如下：

xxxxxxxxxx
7
1
1 def load_data():
2
2     data = load_iris()
3
3     X, y = data.data, data.target
4
4     feature_names = data.feature_names
5
5     X_train, X_test, y_train, y_test = \
6
6         train_test_split(X, y, test_size=0.3, random_state=42)
7
7     return X_train, X_test, y_train, y_test, feature_names

在上述代码中，第4行代码便是得到特征维度的名称，其结果为：

xxxxxxxxxx
1
1
1 ['sepal length(cm)','sepal width(cm)','petal length (cm)','petal width (cm)'] 

2) 训练模型

在完成数据载入后，便可通过类DecisionTreeClassifier来完成决策树的生成。这里除了指定划分标准为'entropy'之外（即使用ID3算法），其它参数保持默认即可：

xxxxxxxxxx
4
1
1 def train(X_train, X_test, y_train, y_test, feature_names):
2
2     model = tree.DecisionTreeClassifier(criterion='entropy')
3
3     model.fit(X_train, y_train)
4
4     print("在测试集上的准确率为：",model.score(X_test, y_test))

训练完成后，可以得到模型在测试集上的准确率为：

xxxxxxxxxx
1
1
在测试集上的准确率为： 1.0

3.2 决策树可视化

当拟合完成决策树后，还可以借助第三方工具graphviz [4]来对生成的决策树进行可视化。具体的，需要下载页面中Windows环境下的ZIP压缩包graphviz-2.46.1-win32.zip。在下载完成并解压成功后，可以得到一个名为Graphviz的文件夹。接着将文件夹Graphviz里的bin目录添加到环境变量中。步骤为右击“此电脑”，点击“属性”，再点击“高级系统设置”，继续点击“环境变量”，最后双击系统变量里的Path变量并新建一个变量输入内容为Graphviz中bin的路径即可，例如掌柜添加时的路径为C: \graphviz-2.46.1-win32\Graphviz\bin。

添加完成环境变量后，再安装graphviz包即可完成可视化的前期准备工作，命令为

xxxxxxxxxx
1
1
pip install graphviz

要实现决策树的可视化，只需要在8.3.1节中train()函数后添加如下代码即可

xxxxxxxxxx
6
1
1     dot_data = tree.export_graphviz(model, out_file=None,
2
2                                     feature_names=feature_names,
3
3                                     filled=True,rounded=True,
4
4                                     special_characters=True)
5
5     graph = graphviz.Source(dot_data)
6
6     graph.render('iris')

在整个代码运行结束后，便会在当前目录中生成一个名为iris.pdf的文件，这就是可视化后的结果，如图8-7所示。

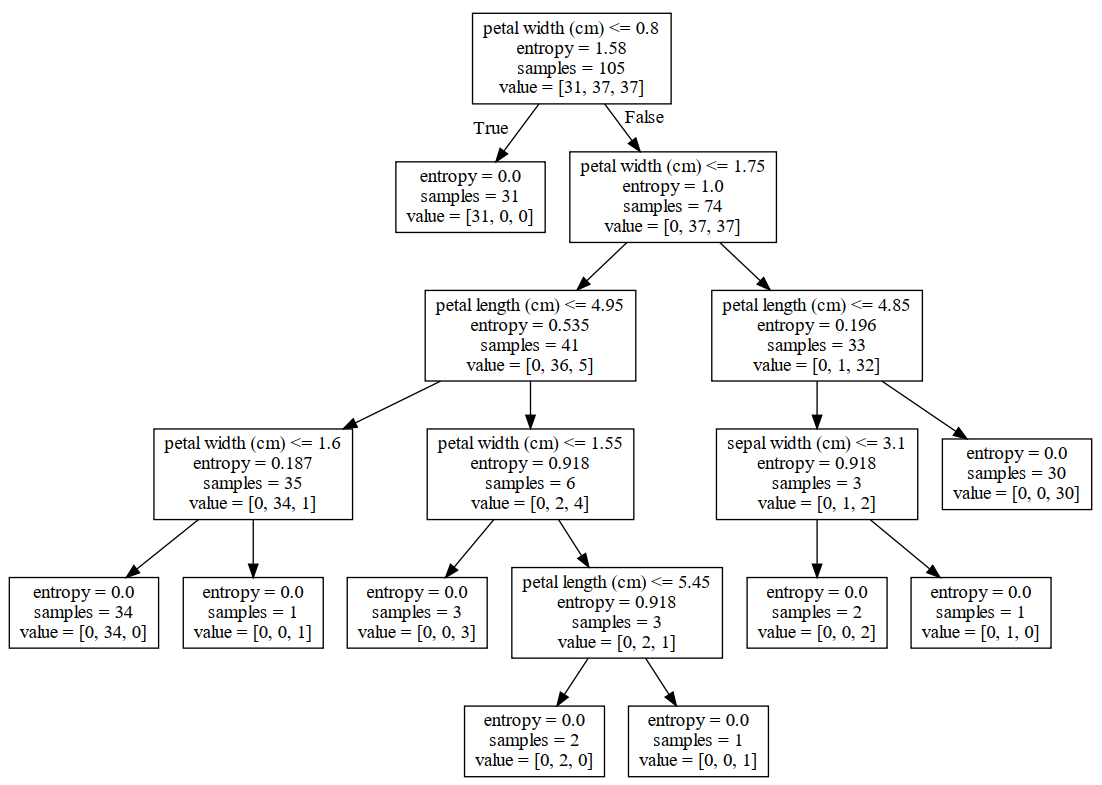
在图8-7中，samples表示当前节点的样本数，value为一个列表表示每个类别对应的样本数。从图中可以看出，随着决策树不断向下分裂，每个节点对应的信息熵总体上也在逐步减小，直到最终变成0结束。

3.3 小结

在本节中，掌柜首先介绍了类DecisionTreeClassifier的使用方法，包括其中一些常见的重要参数及其含义；接着介绍了如何根据现有的数据集来训练一个决策树模型；最后介绍了如何利用开源的graphviz工具来实现决策树的可视化。

4 决策树剪枝

4.1剪枝思想

在8.2节内容中掌柜介绍到，使用ID3算法进行构建决策树时容易产生过拟合现象，因此我们需要使用一种方法来缓解这一现象。通常，决策树过拟合的表现形式为这棵树有很多的叶子节点。想象一下如果这棵树为每个样本点都生成一个叶节点，那么也就代表着这棵树能够拟合所有的样本点，因为决策树的每个叶节点都表示一个分类类别。同时，出现过拟合的原因在于模型在学习时过多地考虑如何提高对训练数据的正确分类，从而构建出了过于复杂的决策树。因此，解决这一问题的办法就是考虑减少决策树的复杂度，对已经生成的决策树进行简化，也就是剪枝（Pruning）。

4.2 剪枝步骤

决策树的剪枝往是通过最小化决策树整体的损失函数或者代价函数来实现。设树$T$$T$的叶节点个数为$|T|$$|T|$，$t$$t$是树$T$$T$的一个叶节点，该叶节点有$N_t$$N_t$个样本点，其中类别$k$$k$的样本点有$N_{tk}$$N_{tk}$个，$k=1,2,...,K,H_t(T)$$k=1,2,...,K,\;\;H_t(T)$为叶节点$t$$t$上的经验熵，$\alpha \ge 0$$\alpha\geq0$为参数，则决策树的损失函数可以定义为

其中经验熵为

进一步有

此时损失函数可以写为

其中$C(T)$$C(T)$表示模型对训练数据的分类误差，即模型与训练集的拟合程度，$|T|$$|T|$表示模型复杂度，参数$\alpha \ge 0$$\alpha\geq0$控制两者之间的平衡。较大的$\alpha$$\alpha$促使选择较简单的模型（树），较小的$\alpha$$\alpha$促使选择较复杂的模型（树）。$\alpha =0$$\alpha=0$意味着只考虑模型与训练集的拟合程度，不考虑模型的复杂度。可以发现，这里$\alpha$$\alpha$的作用就类似于正则化中惩罚系数的作用。

具体的，决策树的剪枝步骤如下

输入：生成算法产生的整个树$T$$T$，参数$\alpha$$\alpha$；

输出：修剪后的子树$T_{\alpha }$$T_{\alpha}$

(1) 计算每个叶节点的经验（信息）熵；

(2) 递归地从树的叶节点往上回溯；设一组叶节点回溯到其父节点之前与之后的整体树分别为$T_B,T_A$$T_B,T_A$，其对应的损失函数值分别是$C_{\alpha }(T_B),C_{\alpha }(T_A)$$C_{\alpha}(T_B),C_{\alpha}(T_A)$，如果$C_{\alpha }(T_A)\le C_{\alpha }(T_B)$$C_{\alpha}(T_A)\leq C_{\alpha}(T_B)$则进行剪枝，即将父节点变为新的叶节点。

(3) 返回(2)，直到不能继续为止，得到损失函数最小的子树$T_{\alpha }$$T_{\alpha}$。

当然，如果仅看这些步骤依旧会很模糊，下面掌柜再来通过一个实际计算示例进行说明。

4.3 剪枝示例

如图8-8所示，在考虑是否要减掉“学历等级”这个节点时，首先需要计算的就是剪枝前的损失函数数值$C_{\alpha }(T_B)$$C_\alpha(T_B)$。由于剪枝时，每次只考虑一个节点，所以在计算剪枝前和剪枝后的损失函数值时，仅考虑该节点即可。因为其它叶节点的经验熵对于剪枝前和剪枝后都没有变化。

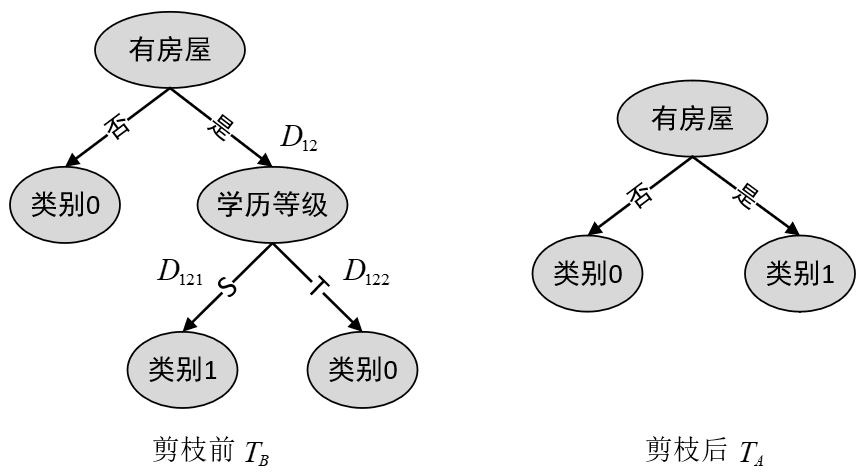
根据表8-3可知，“学历等级”这个节点对应的训练数据如表8-4所示。

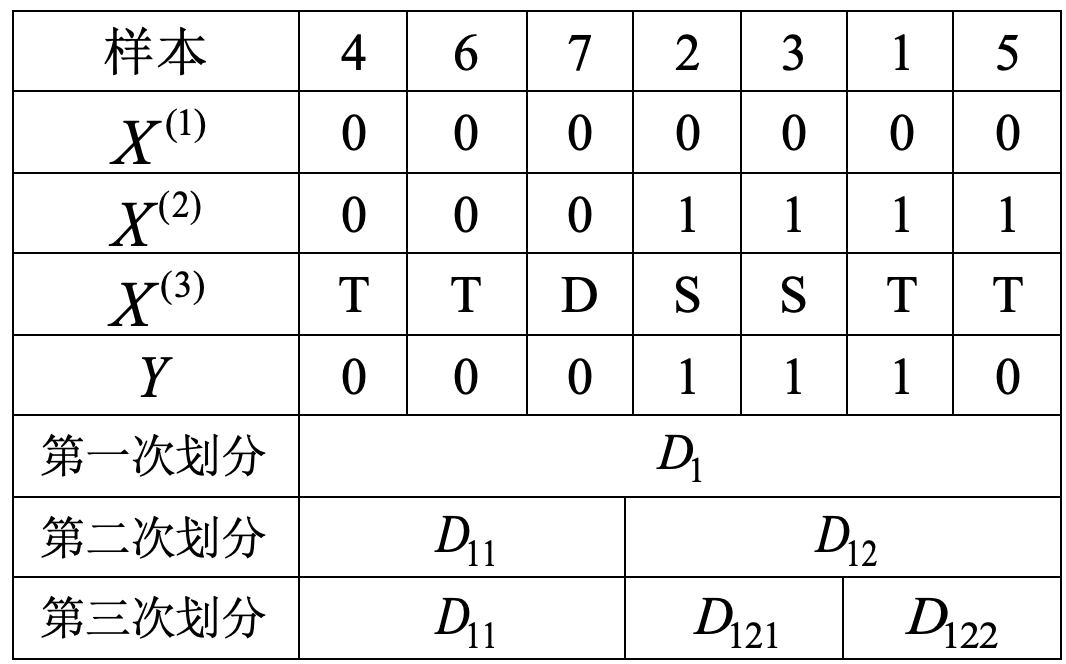
根据式$(8.32)$$(8.32)$有

进一步，根据式$(8.33)$$(8.33)$有

同理可得，剪枝完成后树$T_A$$T_A$损失为

由$(8.35)(8.36)$$(8.35)(8.36)$的结果可知，当设定$\alpha \ge 1.25$$\alpha \ge 1.25$时决策树便会执行剪枝操作，因为此时$C_{\alpha }(T_A)=3.25+\alpha \le$${{C}_{\alpha }}({{T}_{A}})=3.25+\alpha \le$$C_{\alpha }(T_B)=2+2\alpha$${{C}_{\alpha }}({{T}_{B}})=2+2\alpha$满足剪枝条件。

从上述过程可以发现，通过剪枝来缓解决策树的过拟合现象算是一种事后补救的措施，即先生成决策树，然后进行简化处理。但实际上，还可以在决策树生成时就施加相应的条件来避免产生过拟合的现象。例如限制树的深度、限制每个叶节点的最少样本数等，当然这些都可以通过网格搜索来进行参数寻找。在图8-7所示的决策树中，如果将叶节点的最少数量设置为min_samples_leaf=10，那么便可以得到一个更加简单的决策树，如图8-9所示。

4.4 小结

在本节中，笔者首先介绍了决策树中的过拟合现象，阐述了为什么决策树会出现过拟合的现象；然后介绍了可以通过对决策树剪枝来实现缓解决策树过拟合的现象；最后进一步介绍了决策树剪枝的原理以及详细的剪枝计算过程，并且还提到可以通过在构建决策树时施加相应限制条件的方法来避免决策树产生过拟合现象。

本次内容就到此结束，感谢您的阅读！如果你觉得上述内容对你有所帮助，欢迎点赞转发分享！若有任何疑问与建议，请添加掌柜微信nulls8或加群进行交流。青山不改，绿水长流，我们月来客栈见！

引用

[1]吴军，数学之美，人民邮电出版社

[2] 李航，统计机器学习，清华大学出版社

[3]Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825-2830, 2011.

[4] http://www.graphviz.org/download/

推荐阅读

[1] 第1章 机器学习入门之环境安装配置（附高清PDF）

[2] 第2章 从零认识线性回归（附高清PDF与教学PPT）

[3] 第3章 从零认识逻辑回归（附高清PDF与教学PPT）

[4] 第4章 模型的改善与泛化（附高清PDF与教学PPT）

[5] 第5章 K近邻算法（附高清PDF与教学PPT）

[6] 第6章 朴素贝叶斯算法（附高清PDF与教学PPT）

[7]第7章 文本特征提取与模型复用（附高清PDF与教学PPT）