各位朋友大家好,欢迎来到月来客栈,我是掌柜空字符。
在前3章中,笔者分别介绍了线性回归、逻辑回归以及模型的改善与泛化。从这章开始,我们将继续学习下一个新的算法模型——K近邻(K-Nearest Neighbor, KNN),也称为K近邻。那么什么又是K近邻呢?
以下为内容目录,大家可以根据需要进行定位。
5.1 K近邻思想5.2 K近邻原理5.2.1算法原理5.2.2 K值选择5.2.3距离度量5.3 sklearn接口与示例代码5.3.1 sklearn接口介绍2) 训练模型3) 模型预测5.3.2 KNN示例代码2) 模型测试5.3.3 小结5.4 树5.4.1 构造树5.4.2最近邻树搜索5.4.3 最近邻搜索示例5.4.4 K近邻树搜索5.4.5 K近邻搜索示例5.4.6 小结引用推荐阅读
5.1 K近邻思想
某一天,你和几位朋友准备去外面聚餐,但是就晚上吃什么菜一直各持己见。最后,无奈的你提出用多数服从少数的原则来进行选择。于是你们每个人都将自己想要吃的东西写在了纸条上,最后的统计情况是:3个人赞成吃火锅、2个人赞成吃炒菜、1个人赞成吃自助。当然,最后你们一致同意按照多数人的意见去吃了火锅。那这个吃火锅和K近邻有什么关系呢?吃火锅确实跟K近邻没关系,但是整个决策的过程却完全体现了K近邻算法的决策过程。
5.2 K近邻原理
5.2.1算法原理
如图5-1所示,黑色样本点为原始的训练数据,并且包含了0,1,2这3个类别(分别为图中不同形状的样本点)。现在拿到一个新的样本点(图中黑色倒三角),需要对其所属类别进行分类。那K近邻是如何对其进行分类的呢?
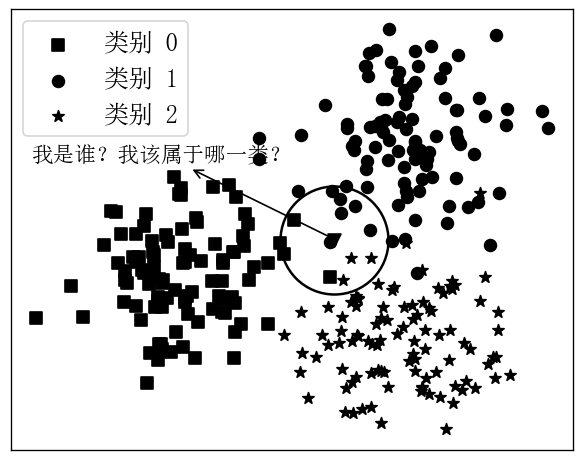
首先KNN会确定一个K值;然后选择离自己(黑色倒三角样本点)最近的K个样本点;最后,根据投票的规则(Majority Voting Rule)确定新样本应该所属的类别。如图5-1所示,示例中选择了离三角形样本点最近的14个样本点(方形4个、圆形7个、星形3个)。并且在图中,离三角形样本点最近的14个样本中 最多的为圆形样本,所以KNN算法将把新样本归类为类别1。
因此,对于K近邻算法的原理可以总结为如下三个步骤:
1) 首先确定一个K值;
用于选择离自己(三角形样本点)最近的样本数。
2) 然后选择一种度量距离;
用来计算得到离自己最近的K个样本,示例中采用了应用最为广泛的欧氏距离。
3) 最后确定一种决策规则;
用来判定新样本所属类别,示例中采用了基于投票的分类规则。
可以看出,KNN分类的3个步骤其实也就对应了3个超参数的选择。但是,通常来说对于决策规则的选择基本上都是采用了基于投票的分类规则,因此下面对于这个问题也就不再进行额外的讨论。
5.2.2 K值选择
K值的选择会极大程度上影响KNN的分类结果。如图5-2所示,可以想象如果在分类过程中选择较小的K值,将会使得模型的训练误差减小而使得模型的泛化误差增大,也就是模型过于复杂而产生了过拟合现象。当选择较大的K值时,将使得模型趋于简单,容易发生欠拟合的情况。极端情况下,如果直接将K值设置为样本总数,那么无论新输入的样本点位于什么地方,模型都将会简单地预测它为训练样本最多的类别,且会恒定不变。因此,对于K值的选择,依然建议使用第4章介绍的交叉验证方法进行选择。

5.2.3距离度量
在样本空间中,任意两个样本点之间的距离都可以看作是两个样本点之间相似性的度量。两个样本点之间的距离越近,也就也就意味着这两个样本点越相似。在第10章介绍聚类算法时,同样也会用到样本点间相似性的度量。同时,不同的距离度量方式将会产生不同的距离,进而最后产生不同的分类结果。虽然一般情况下KNN使用的都是欧式距离,但也可以是其它距离,例如更一般的距离或者Minkowski距离[1]。
设训练样本其中,即每个样本包含个特征维度,则距离定义为
当时称为曼哈顿(Manhattan distance),即
从式可以看出,曼哈顿距离计算的是各个维度之间距离的绝对值累加和。
当时称为欧氏距离(Euclidean distance),即
当时,它是各个坐标距离中的最大值,即
当然,同样能取其它任意的正整数,然后按照式进行计算即可。
例如现有二维空间的3个样本点,,则其在不同取值下,距离样本点最近邻的点为
由式可知,当时,离样本点最近的样本点分别是。
5.3 sklearn接口与示例代码
5.3.1 sklearn接口介绍
在正式介绍如何用sklearn库来完成KNN的建模任务前,笔者先来总结一下sklearn的使用方法,这样更加有利于后续内容的学习。
根据第2、3、4章中的示例代码可以发现,sklearn在实现各类算法模型时基本上都遵循了统一的接口风格,这使得我们在刚开始学习的时候很容易就能入门上手。总结起来,在sklearn中对于各类模型的使用,基本上都遵循以下3个步骤:
1) 建立模型
这一步通常来说都是通过在对应的路径下导入我们需要用到的模型类,例如可以通过如下一行代码来导入一个基于梯度下降算法优化的分类器。
xxxxxxxxxx11from sklearn.linear_model import SGDClassifier在导入模型类后,需要通过传入模型对应的参数来实例化这个模型,例如可以通过如下一行代码来实例化一个逻辑回归模型。
xxxxxxxxxx11model = SGDClassifier(loss='log', penalty='l2', alpha=0.5)同时,由于sklearn在迭代更新中可能会更改一些接口的名称或者位置,具体的路径信息可以查看官方的API说明文档[2]。
2) 训练模型
在sklearn中,所有模型的训练(或者计算)过程都是通过model.fit()这个方法来完成。并且一般情况下需要按实际情况在调用model.fit()时传入相应参数。如果是有监督模型则一般是model.fit(x,y),无监督则是mode.fit(x)。同时,还可可以调用model.score(x,y)来对模型的结果进行评估。
3) 模型预测
在训练好一个模型后,通常都要对测试集或者新输入的数据进行预测。在sklearn中一般都是通过模型类对应的model.predict(x)方法来实现的。但这也不是绝对,例如对数据进行预处理时,在调用model.fit()方法在训练集上计算得到相应的参数后,往往是通过model.transform()方法来对测试集(或新数据)进行的变换。
总体上来讲,在sklearn中基本上所有的算法模型都可以通过上面这3个步走来完成对模型的建立、训练与预测。
5.3.2 KNN示例代码
从5.2节的分析可知,其实KNN在分类过程中并没有同之前算法模型一样,有一个训练求解参数的过程。这是因为KNN算法根本就没有可训练的参数,仅仅只有3个超参数。而KNN算法的核心在于如何快速的找到距离任意一个样本最近的K个样本点。当然,最直接的办法就是挨个遍历样本点计算距离,但是当样本点达到一定数量级后这种做法显然是行不通。所以此时可以通过建立KD树(KDTree)或者是Ball树(BallTree)来解决这一问题。不过这里暂时不做介绍,先直接通过开源库sklearn来实现。
本次示例的数据集仍旧采用第4章中介绍的手写体分类数据集。同时,在下面示例中笔者将介绍如何通过网格搜索(Grid Search)来快速完成模型的选择,完整代码见Chapter05/01_knn_train.py文件。
1) 模型选择
由于在4.6.1节中已经详细介绍过了该数据集的载入和预处理方法,所以这里就不再赘述。从上面的分析可以,KNN算法一共有两个(另外一个暂不考虑)超参数,即K值和度量方式P值。假设两者的取值分别为n_neighbors = [5, 6, 7, 8, 9, 10],p=[1, 2],则此时一共就有12个备选模型。同时,如果采用5折交叉验证,则一共要进行60次的模型拟合,并且需要3个循环来实现。不过好在sklearn中提供了网格所搜的功能可以帮助我们通过4行代码就实现上述功能,代码如下:
xxxxxxxxxx81from sklearn.neighbors import KNeighborsClassifier2from sklearn.model_selection import GridSearchCV3def model_selection(x_train, y_train):4 paras = {'n_neighbors': [5, 6, 7, 8, 9, 10], 'p': [1, 2]}5 model = KNeighborsClassifier()6 gs = GridSearchCV(model, paras, verbose=2, cv=5)7 gs.fit(x_train, y_train)8 print('最佳模型:', gs.best_params_, ‘准确率:’,gs.best_score_)在上述代码中,第4行以字典的形式定义了超参数的取值情况,并且需要注意的是,
字典的key必须是类KNeighborsClassifier中参数的名字。其中,类KNeighborsClassifier就是sklearn中所实现的KNN算法模型。因此,该类也包含了KNN中最基本的两个参数K值和P值。第5行定义了一个KNN模型,但值得注意的是此时并没有在定义模型的时候就传入相应的参数,即以KNeighborsClassifier(n_neighbors = 2, p = 2)这样的形式(其中n_neighbors就是K值)来实例化这个类。因为在使用网格搜索时,需要将模型作为一个参数传入到GridSearchCV这个类中,同时也需要将模型对应的超参数以字典的形式传入。第6行在实例化GridSearchCV这个类时便传入了定义的KNN模型以及参数字典,其中verbose用来控制训练过程中输出提示信息的详细程度,cv=5表示在训练过程中使用5折交叉验证。最后,根据传入的训练集,便可以对模型进行训练。
在模型训练完成后,便可以输出最佳模型(超参数组合),以及此时对应的模型得分,如下所示
xxxxxxxxxx61Fitting 5 folds for each of 12 candidates, totalling 60 fits2[CV] END ...................n_neighbors=5, p=1; total time= 0.0s3[CV] END ...................n_neighbors=5, p=2; total time= 0.0s4.....5.....6最佳模型: {'n_neighbors': 5, 'p': 1 准确率:0.971}从最终的输出结果可知,当数K取值为5且P取值为1时所对应的模型最佳。同时,由于模型在进行交叉验证时各个拟合过程之间相互独立的,为了提高整个过程的训练速度,GridSearchCV还支持以并行的方式进行参数搜索。当在实例化类GridSearchCV时,只需要同时指定n_jobs=2即可实现参数的并行搜索,它表示同时使用CPU的两个核来进行计算。当然也可以指定为-1,即使用所有的核同时进行计算。
2) 模型测试
在经过网格搜索得到最优参数组合后,便可以再拿完整的训练集重新再训练一次模型,然后再来评估其在测试集上的泛化误差。当然,在这里也可以直接使用GridSearchCV中的predict()和score()方法来得到测试集的预测结果以及对应的准确率,即gs.predict(x_test)和gs.score(x_test,y_test)。
xxxxxxxxxx61def train(x_train, x_test, y_train, y_test):2 model = KNeighborsClassifier(5, p=1)3 model.fit(x_train, y_train)4 y_pred = model.predict(x_test)5 print(classification_report(y_test,y_pred))6 print("Accuracy: ", model.score(x_test, y_test)) # 0.963这样,便能够得到模型在测试集上的泛化误差。
5.3.3 小结
在这节内容中,文章笔者首先通过一个引例介绍了KNN分类器的主要思想;接着介绍了K值对算法结果的影响,以及介绍了衡量样本间距离的不同度量方式;最后笔者通过开源的sklearn框架介绍了如何建模使用KNN分类器,并同时还总结了sklearn中模型使用的3个步骤以及如何使用GridSearch来实现超参数的并行搜索。
5.4 树
在前面几节内容在,笔者分别介绍了KNN分类器的基本原理以及其如何通过开源的sklearn框架来实现KNN的建模。不过到目前为止,还有一个问题没有解决的就是如何快速的找到当前样本点周围最近的K个样本点。通常来说,这一问题可以通过树来解决,下面开始介绍其具体原理。
5.4.1 构造树
树(-Dimensional Tree)是一种空间划分数据结构,用于组织维空间中的点,其本质上也就等同于二叉搜索树。不同的是,在树中每个节点存储的并不是一个值,而是一个维的样本点[3]。在二叉搜索树中,任意节点中的值都大于其左子树中的所有值,小于或等于其右子树中的所有值,如图5-3所示。
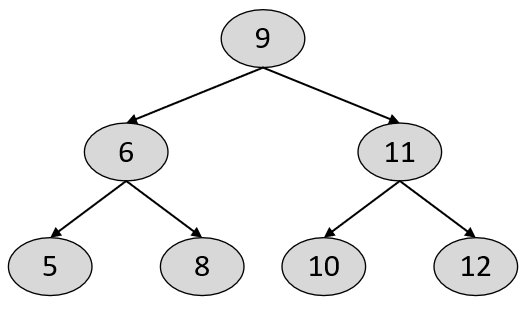
在树,所有的节点也都满足类似二叉搜索树的特性,即左子树中所有的样本点均“小于”其父节点中的样本点,而右子树中所有的样本点均“大于”或“等于”其父节点中的样本点。因此可以看出,构造树的关键就在于如何定义任意两个维样本点之间的大小关系。
具体的,在构造树时,每一层的节点在划分左右子树时只会循环的选择维中的其中一个维度进行比较。例如样本点中一共有两个维度,那么在对根节点进行划分时可以以维度对左右子树进行划分;接着再以维度对根节点的孩子进行左右子树划分;进一步,根节点的孩子的孩子再以维度进行左右子树划分,以此循环[4]。同时,为了使得最后得到的是一棵平衡的树,所以在的构建过程中每次都会选择当前子树中对应维度的中位数作为切分点。
例如现在有样本点[5,7], [3,8], [6,2], [8,5], [15,6], [10,4], [12,13], [9,10],[11,14],那么根据上述规则便可以构造得到如图5-4所示的树。
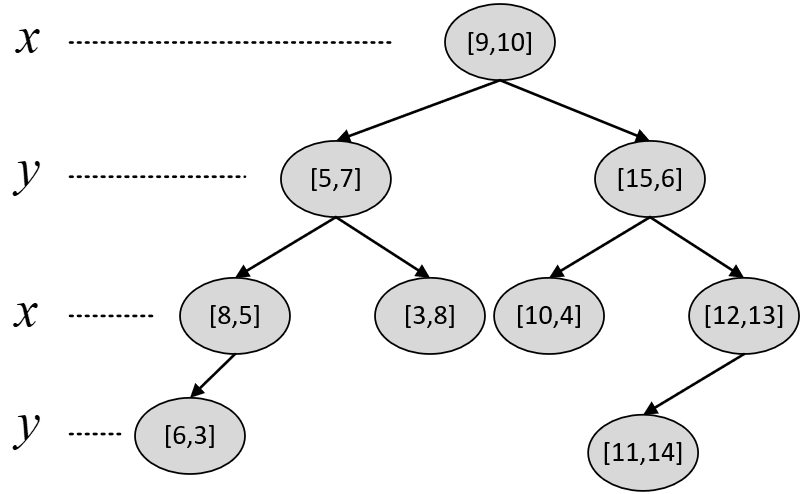
图5-4 树示例
从图5-4可以看出,对于根节点来说其左子树中所有样本点的维度均小于9,其右子树的维度均大于等于9;对于根节点的左孩子来说其左子树中所有样本点的维度均小于7,其右子树中所有样本点的维度均大于等于7。当然,对于其它节点也都满足类似的特性。同时,根据树交替选择特征维度对样本空间进行划分的特性,以图5-4中的划分方式还能得到如图5-5所示的特征空间。
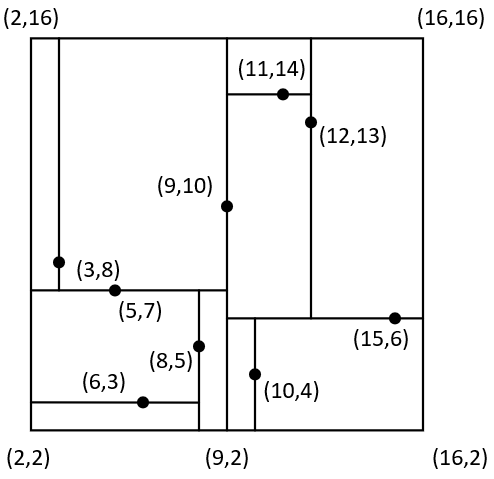
图5-5 树特征空间
从图5-5中可以看出,整个二维平面首先被样本点[9,10]划分成了左右两个部分(对应图5-4中的左右子树),接着左右两个部分又各自分别被[5,7]和[15,6]划分成了上下两个部分,直到划分结束。到此,对于树的构造就介绍完了,接下来看如何通过树来完成搜索任务。
5.4.2最近邻树搜索
在正式介绍K近邻(即最近的K个样本点)搜索前,笔者先来介绍如何利用树进行最近邻搜索。总的来说,在已知树中搜索离给定样本点最近的样本点时,首先设定一个当前全局最佳点和一个当前全局最短距离,分别用来保存当前离最近的样本点以及对应的距离;然后从根节点开始以类似生成树的规则来递归的遍历树中的节点,如果当前节点离的距离小于全局最短距离,那么更新全局最佳点和全局最短距离;如果被搜索点到当前节点划分维度的距离小于全局最短距离,那么再递归遍历当前节点另外一个子树,直至整个递归过程结束。具体步骤可以总结为[4]:
(1) 设定一个当前全局最佳点和全局最短距离,分别用来保存当前离搜索点最近的样本点和最短距离,初始值分别为空和无穷大;
(2) 从根节点开始,并设其为当前节点;
(3) 如果当前节点为空,则结束;
(4) 如果当前节点到被搜索点的距离小于当前全局最短距离,则更新全局最佳点和最短距离;
(5) 如果被搜索点的划分维度小于当前节点的划分维度,则设当前节点的左孩子为新的当前节点并执行步骤(3)(4)(5)(6);反之设当前节点的右孩子为新的当前节点并执行步骤(3)(4)(5)(6);
(6) 如果被搜索点到当前节点划分维度的距离小于全局最短距离,则说明全局最佳点可能存在于当前节点的另外一个子树中,所以设当前节点的另外一个孩子为当前节点并执行步骤(3)(4)(5)(6);
递归完成后,此时的全局最佳点就是在树中离被搜索点最近的样本点。
这里需要明白一点的是,利用步骤(6)中的规则来判断另外一个子树中是否可能存在全局最佳点的原理如图5-6所示。
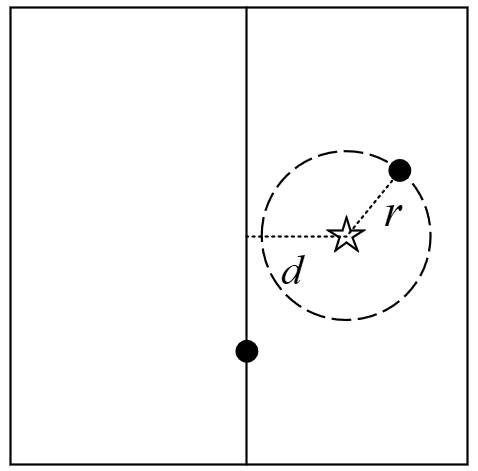
在图5-6中,右上角为当前全局最佳点,五角星为被搜索点。可以看到,此时的整个空间被下方的样本点划分成了左右两个部分(子树)。并且,五角星离左子树中样本点的最短距离为五角星到当前划分维度的距离。显然,如果被搜索点到当前全局最佳点的距离小于距离,那么此时左子树中就不可能存在更优的全局最佳点。
当然,上述步骤还可以通过一个更清晰的伪代码来进行表达:
xxxxxxxxxx131bestNode, bestDist = None, inf2def NearestNodeSearch(curr_node):3 if curr_node == None:4 return5 if distance(curr_node, bestNode) <bestDist:6 bestDist = distance(curr_node, bestNode)7 bestNode = curr_node8 if q_i < curr_node_i:9 NearestNodeSearch(curr_node.left)10 else:11 NearestNodeSearch(curr_node.right)12 if |curr_node_i - q_i| < bestDist:13 NearestNodeSearch(curr_node.other)在上述代码中,q_i和curr_node_i分别表示被搜索点和当前节点的划分维度;curr_node.other表示curr_node.left和curr_node.right中先前未被访问过的子树。
5.4.3 最近邻搜索示例
在介绍完最近邻的搜索原理后再来看几个实际的搜索示例,以便对搜索过程有更加清晰的理解。如图5-7所示,左右两边分别是5.4.1节中所得到的树和特征划分空间,同时右图中的五角星为给定的被搜索点,接下来开始在左边的树中搜索离点最近的样本点。
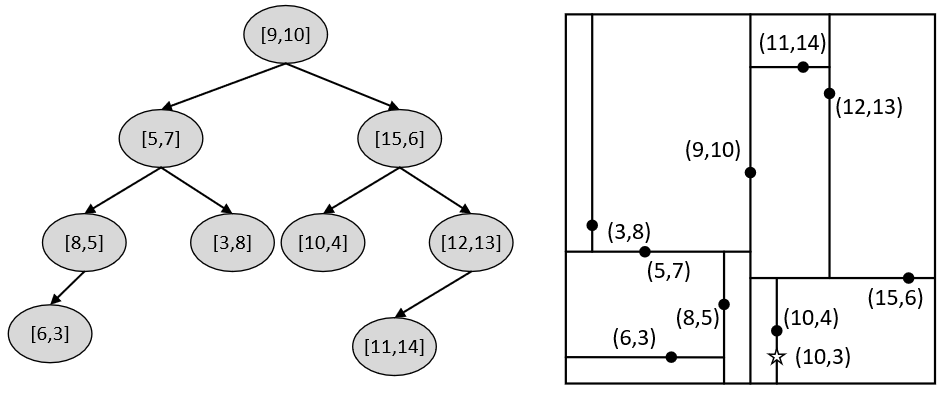
在搜索伊始,全局最佳点和全局最短距离分别为空和无穷大。第1次递归:此时设根节点[9,10]为当前节点,因满足步骤(4)当前节点到被搜索点的距离小于当前全局最短距离,所以更新当前最佳点为[9,10],全局最短距离为7.07。接着,由于被搜索点的划分维度10大于当前节点的划分维度9,因此设当前节点的右孩子[15,6]为新的当前节点。第2次递归:继续执行步骤(4),由于此时当前节点到被搜索点的距离为5.83,小于全最最短距离,所以更新当前最佳点为[15,6],全局最短距离为5.83。进一步,由于被搜索点的划分维度3小于当前节点的划分维度6,因此设当前节点的左孩子[10,4]为新的当前节点。第3次递归:继续执行步骤(4),由于此时当前节点到被搜索点的距离为1,小于全最最短距离,所以更新当前最佳点为[10,4],全局最短距离为1。此时,由于被搜索点的划分维度10大于等于当前节点的划分维度10,因此设当前节点的右孩子为新的当前节点,并进入第4次递归。
第4次递归:由于此时当前节点为空,所以第4次递归结束返回第3次递归,即此时的当前节点为[10,4],并继续执行步骤(6)。由于被搜索点[10,3]到当前划分维度的距离为0,小于全局最短距离1,说明全局最佳点可能存在于当前节点的左子树中(此时可以想象假如树中存在点[9.9,3]),所以设当前节点的左孩子为新的当前节点。第5次递归:由于当前节点为空,所以第5次递归结束回到第3次递归中。返回第3次递归后,此时的当前节点为[10,4],且已执行完步骤(6),返回到第2次递归中。返回第2次递归后,此时的当前节点为[15,6],并继续执行步骤(6)。由于被搜索点[10,3]到当前划分维度的距离为3,大于全局最短距离,则说明节点[15,6]的右子树中不可能存在全局最佳点,此时返回到第1次递归中。返回第1次递归后,此时的当前节点为根节点[9,10],并继续执行步骤(6)。由于被搜索点[10,3]到当前划分维度的距离为1,大于等于全局最短距离1,所以当前节点的左子树中不可能存在全局最佳点。到此步骤(6)执行结束,即所有的递归过程都执行完毕。此时的全局最佳点中保存的点[10,4]便是树中离被搜索点[10,3]最近的样本点。
经过上述步骤后,相信读者朋友们对于树的搜索过程已经有了清晰的认识。同时,各位读者也可以自己来试着从上述树中来搜索离[8.9,4]最近的样本点。在搜索过程中会发现,一开始会从根节点进入左子树,并找到[8,5]为当前全局最佳点。但是当一步步回溯后会发现,原来右子树中的[10,4]才是真正离[8.9,4]最近的样本点。
5.4.4 K近邻树搜索
在介绍完最近邻的树搜索原理后便可以轻松的理解K近邻的树搜索过程。需要注意的是,这里的两个“K”分别表示两种不同的含义,前者表示要搜索得到离给定点最近的K个样本点,而后者表示的是样本点的维度。
总的来说K近邻的搜索过程和最近邻的搜索过程类似,只是需要额外的维护一个大小为K的有序列表。在整个列表中,当前距离被搜索点最近的样本点放在首位,而距离被搜索点最远的样本点放在末尾。具体的搜索过程可以总结为:
(1) 设定大小为K的有序列表用来保存当前离搜索点最近的K个样本点;
(2) 从根节点开始,并设其为当前节点;
(3) 如果当前节点为空,则结束;
(4) 如果列表不满,则直接将当前样本插入到列表中;如果列表已满,则判断当前样本到被搜索点的距离是否小于列表最后一个元素到被搜索点的距离,成立则将列表中最后一个元素删除,并插入当前样本;(每次插入后仍有序)
(5) 如果被搜索点的划分维度小于当前节点的划分维度,则设当前节点的左孩子为新的当前节点并执行步骤(3)(4)(5)(6);反之设当前节点的右孩子为新的当前节点并执行步骤(3)(4)(5)(6);
(6) 如果列表不满,或者如果被搜索点到当前节点划分维度的距离小于列表中最后一个元素到被搜索点的距离,则设当前节点的另外一个孩子为当前节点并执行步骤(3)(4)(5)(6);
递归完成后,此时离被搜索点最近的K个样本点就是有序列表中的K个元素。
上述步骤同样可以通过一个更清晰的伪代码来进行表达:
xxxxxxxxxx161KNearestNodes, n = [], 02def NearestNodeSearch(curr_node):3 if curr_node == None:4 return5 if n < K:6 KNearestNodes.insert(curr_node) # 插入后保持有序7 if n >= K and8 distance(curr_node, q) < distance(curr_node, KNearestNodes[-1]):9 KNearestNodes.pop()10 KNearestNodes.insert(curr_node) # 插入后保持有序11 if q_i < curr_node_i:12 NearestNodeSearch(curr_node.left)13 else:14 NearestNodeSearch(curr_node.right)15 if n < K or | curr_node_i - q_i | < distance(q, KNearestNodes[-1]):16 NearestNodeSearch(curr_node.other)在上述代码中,KNearestNodes[-1]表示取有序列表中的最后一个元素;q_i和curr_node_i分别表示被搜索点和当前节点的划分维度;curr_node.other表示curr_node.left和curr_node.right中先前未被访问过的子树。
5.4.5 K近邻搜索示例
下面,以图5-7中的树为例,来搜索离[10,3]最近的3个样本点。
在搜索伊始,有序列表为空,K为3。第一次递归:此时设根节点[9,10]为当前节点,因满足步骤(4)中的列表为空的条件,所以直接将根节点加入列表中,即此时KNearestNodes=([9,10])。接着,由于被搜索点的划分维度10大于当前节点的划分维度9,因此设当前节点的右孩子[15,6]为新的当前节点。第2次递归:继续执行步骤(4),由于此时列表未满,所以直接将当前节点插入列表中,即此时KNearestNodes=([15,6], [9,10])。进一步,由于被搜索点的划分维度3小于当前节点的划分维度6,因此设当前节点的左孩子[10,4]为新的当前节点。第3次递归:继续执行步骤(4),由于此时列表未满,所以直接将当前节点插入列表中,且由于[10,4]当前离被搜索点最近,所以应该放在列表最前面,即此时KNearestNodes=([10,4], [15,6], [9,10])。进一步,由于被搜索点的划分维度10大于等于当前节点的划分维度10,所以设当前节点的右孩子为新的当前节点,并进入第4次递归。
第4次递归:由于此时当前节点为空,所以第4次递归结束并返回到第3次递归中,即此时的当前节点为[10,4],并继续执行步骤(6)。此时列表已满,但由于被搜索点[10,3]到当前划分维度的距离为0,小于被搜索点到有序列表中最后一个样本点距离,说明可能存在一个比有序列表中最后一个元素更佳的样本点。所以设当前节点的左孩子为新的当前节点。第5次递归:由于当前节点为空,所以第5次递归结束回到第3次递归中。返回到第3次递归后,此时的当前节点为[10,4],且已执行完步骤(6),返回到第2次递归中。返回到第2次递归后,此时的当前节点为[15,6],并继续执行步骤(6)。此时列表已满,但由于被搜索点[10,3]到当前划分维度的距离为3,小于被搜索点到[9,10]的距离7.07,说明在当前节点[15,6]的右子树中可能存在一个比[9,10]更佳的样本点。所以设[15,6]的右孩子[12,13]为新的当前节点。第6次递归:此时列表已满,且由于当前节点到被搜索点的距离10.19,大于被搜索点到[9,10]的距离,所以继续执行步骤(5)。由于被搜索点的划分维度10小于当前节点的划分维度12,所以设[11,14]为新的当前节点,并进入第7次递归。
第7次递归:此时列表已满,且由于当前节点到被搜索点的距离11.04,大于被搜索点到[9,10]的距离,所以继续执行步骤(5)。由于被搜索点的划分维度3小于当前节点的划分维度14,所以设[11,14]的左孩子为新的当前节点。第8次递归:由于此时当前节点为空,所以第8次递归结束并返回到第7次递归中,即此时的当前节点为[11,14],并继续执行步骤(6)。此时列表已满,且由于被搜索点[10,3]到当前划分维度的距离为11,大于被搜索点到有序列表中最后一个样本点距离,所以第7次递归结束并回到第6次递归。
返回第6次递归后,此时的当前节点为[12,13],继续执行步骤(6)。此时列表已满,且由于被搜索点[10,3]到当前划分维度的距离为2,小于被搜索点到有序列表中最后一个样本点的距离,说明当前节点[12,13]的右子树中存在比[9,10]更近的点(可以想象假设存在点[12.1,6.1]),所以设[12,13]的右孩子为新的当前节点。第9次递归:由于此时当前节点为空,所以第9次递归结束并返回到第6次递归中,即此时的当前节点为[12,13],且已经执行完步骤(6),进而返回到第2次递归。返回到第2次递归后,此时的当前节点为[15,6],且已执行完步骤(6),进而返回到第1次递归中。
返回第1次递归后,此时的当前节点为[9,10],继续执行步骤(6)。此时列表已满,但由于被搜索点[10,3]到当前划分维度的距离为1,小于被搜索点到有序列表中最后一个样本点的距离,说明当前节点[9,10]的左子树中存在比[9,10]更近的点(从图5-7中一眼便能看出,例如点[8,5]),所以设[5,7]为新的当前节点。第10次递归:此时列表已满,但由于当前节点到被搜索点的距离6.4,小于被搜索点到有序列表中最后一个样本点[9,10]的距离7.07,因此更新KNearestNodes=([10,4], [15,6], [5,7]),并继续执行步骤(5)。由于被搜索点的划分维度3小于当前节点的划分维度7,所以设[8,5]为新的当前节点,并进入第11次递归。
第11次递归:此时列表已满,但由于当前节点到被搜索点的距离2.83,小于被搜索点到有序列表中最后一个样本点[5,7]的距离6.4,因此更新KNearestNodes=([10,4], [8,5], [15,6]),并继续执行步骤(5)。由于被搜索点的划分维度10大于当前节点的划分维度8,所以设[8,5]的右孩子为新的当前节点。第12次递归:由于此时当前节点为空,所以第12次递归结束并返回到第11次递归中,即此时的当前节点为[8,5],并继续执行步骤(6)。此时列表已满,但由于被搜索点[10,3]到当前划分维度的距离为2,小于被搜索点到有序列表中最后一个样本点的距离,所以设[6,3]为新的当前节点,并进入第13次递归。
第13次递归:此时列表已满,但由于当前节点到被搜索点的距离4.0,小于被搜索点到有序列表中最后一个样本点[15,6]的距离5.83,因此更新KNearestNodes=([10,4], [8,5], [6,3]),并继续执行步骤(5)。由于被搜索点的划分维度3大于等于当前节点的划分维度3,所以设[6,3]的右孩子为新的当前节点。第14次递归:由于此时当前节点为空,所以第14次递归结束并返回到第13次递归中,即此时的当前节点为[6,3],并继续执行步骤(6)。此时列表已满,但由于被搜索点[10,3]到当前划分维度的距离为0,小于被搜索点到有序列表中最后一个样本点的距离,说明[6,3]的左子树中存在比[6,3]更近的点(可以想象假设存在点[7,2.9]),所以设[6,3]的左孩子为新的当前节点,并进入第15次递归。
第15次递归:由于此时当前节点为空,所以第15次递归结束并返回到第13次递归中,即此时的当前节点为[6,3],且已经执行完步骤(6)进一步返回第11次递归中。返回第11次递归后,此时的当前节点为[8,5],且已经执行完步骤(6)进一步返回第10次递归中。返回第10次递归后,当前节点为[5,7],继续执行步骤(6)。由于此时列表已满,且被搜索点[10,3]到当前划分维度的距离4,大于等于被搜索点到有序列表中最后一个样本点[6,3]的距离,所以[5,7]的右子树中不可能存在比[6,3]更近的点,故返回第1次递归。
在返回到第1次递归后,此时的当前节点为[9,10],且已执行完步骤(6),即所有的递归过程结束。此时有序列表中的元素便为树中离被搜索点[10,3]最近的3个样本点,即KNearestNodes=([10,4], [8,5], [6,3])。整个递归过程顺序如图5-8所示。
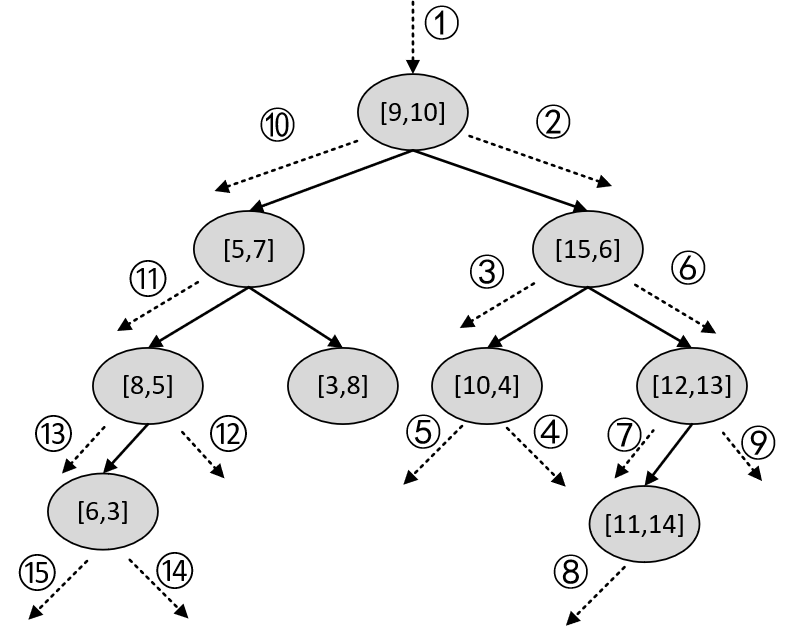
到此,对于K近邻算法的原理就介绍完了。
5.4.6 小结
在本节中,笔者首先介绍了树的基本原理,以及如何来构造一棵树;接着介绍了如何通过树来搜索离给定点最近的样本点,并通过一个实际的搜索示例来进行了详细的介绍;最后介绍了如何在最近邻的基础上,在树中来搜索离给定点最近的K个样本点,即K近邻搜索。
总结一下,在本章中笔者首先介绍了K近邻算法的主要思想及其原理,包括K值选择和距离的度量方式等;接着简单的总结了sklearn框架接口的设计风格以及通用的建模步骤;然后介绍了如何通过sklearn来建立完整的KNN分类器,包括模型训练、模型选择、并行搜索和交叉验证等;最后详细介绍了如何通过树来实现KNN中K近邻样本点的搜索。
本次内容就到此结束,感谢您的阅读!如果你觉得上述内容对你有所帮助,欢迎分享至一位你的朋友!若有任何疑问与建议,请添加笔者微信'nulls8'或加群进行交流。青山不改,绿水长流,我们月来客栈见!
引用
[1]《统计机器学习》李航
[2]Scikit-learn: Machine Learning in Python, Pedregosa et al., JMLR 12, pp. 2825-2830, 2011.
[3]https://en.wikipedia.org/wiki/K-d_tree
[4]http://web.stanford.edu/class/cs106l/
推荐阅读
[2] 第2章 从零认识线性回归(附高清PDF与教学PPT)