1 引言
各位朋友大家好,欢迎来到月来客栈。今天要和大家介绍的是论文”Attention is all you need“解读系列文章的第2部分,也就是Transformer的网络结构以及位置编码。经过上一篇文章[1]的介绍,我们对于多头注意力机制已经有了一个比较清晰的认识。接下来,我们就来看看如何通过多头注意力机制来构造编码器和解码器,以及最后的Transformer模型。
2 Embedding
在正式介绍Transformer的网络结构之前,我们先来一起看看Transformer是如何对字符进行Embedding的。
2.1 Token Embedding
熟悉文本处理的读者可能都知道,在对文本相关的数据进行建模时首先要做的便是对其进行向量化。例如在机器学习中,常见的文本表示方法有one-hot编码、词袋模型以及TF-IDF等。不过在深度学习中,更常见的做法便是将各个词(或者字)通过一个Embedding层映射到低维稠密的向量空间。因此,在Transformer模型中,首先第一步要做的同样是将文本以这样的方式进行向量化表示,并且将其称之为Token Embedding,如图1所示。

如果是换做之前的网络模型,例如CNN或者RNN,那么对于文本向量化的步骤就到此结束了,因为这些网络结构本身已经具备了捕捉时序特征的能力。但是这对仅仅只有自注意力机制的网络结构来说却不行。为什么呢?经过上一篇文章对自注意力机制的介绍我们知道,自注意力机制在实际运算过程中不过就是几个矩阵来回相乘进行线性变换而已。因此,这就导致即使是打乱各个词的顺序,那么最终计算得到的结果本质上却没有发生任何变换,换句话说仅仅只使用自注意力机制会丢失文本原有的序列信息。

如图2所示,在经过词嵌入表示后,序列“我 在 看 书”经过了一次线性变换。现在,我们将序列变成“书 在 看 我”,然后同样以中间这个权重矩阵来进行线性变换,过程如图3所示。
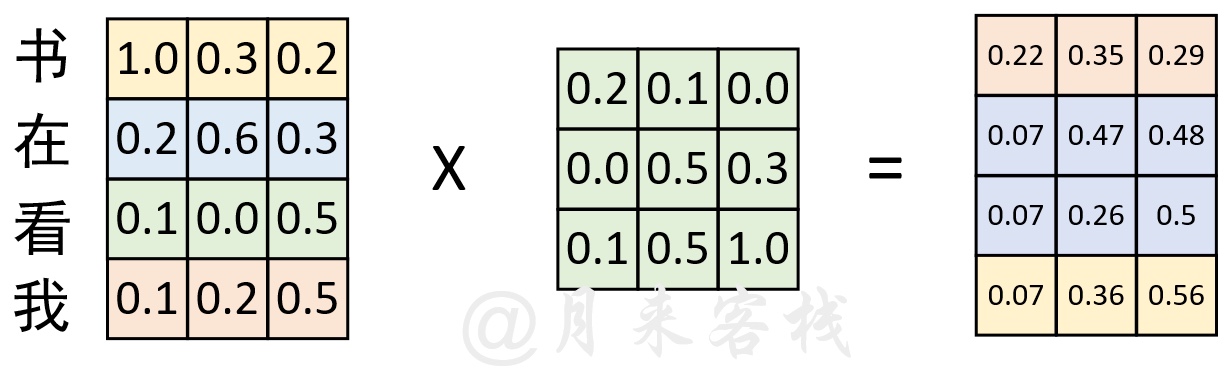
根据图3中的计算结果来看,序列在交换位置前和交换位置后计算得到的结果在本质上并没有任何区别,仅仅只是交换了对应的位置。因此,基于这样的原因,Transformer在原始输入文本进行Token Embedding后,又额外的加入了一个Positional Embedding来刻画数据在时序上的特征。
Since our model contains no recurrence and no convolution, in order for the model to make use of the order of the sequence, we must inject some information about the relative or absolute position of the tokens in the sequence.
2.2 Positional Embedding
说了这么多,那到底什么又是Positional Embedding呢?数无形时少直觉,下面我们先来通过一幅图直观看看经过Positional Embedding处理后到底产生了什么样的变化。
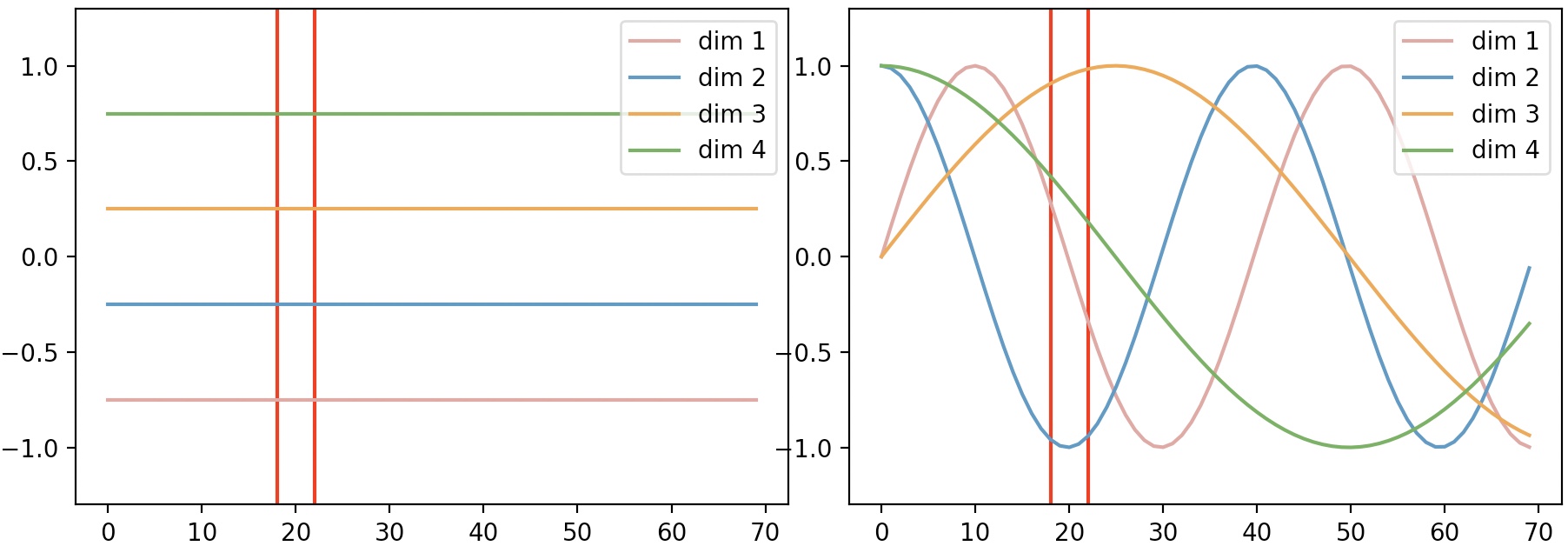
如图4所示,横坐标表示序列中每一个粒度的位置,每一条曲线或者直线表示每个维度对应的位置信息。在左图中,每个维度所对应的位置信息都是一个不变的常数;而在右图中,每个维度所对应的位置信息都是基于某种公式变换所得到。换句话说就是,左图中任意两个位置上的向量都可以进行交换而模型却不能捕捉到这一差异,但是加入右图这样的位置信息模型却能够感知到。例如位置20这一处的向量,在左图中无论你将它换到哪个位置,都和原来一模一样;但在右图中,你却再也找不到与位置20处位置信息相同的位置。
下面,笔者通过两个实际的示例来进行说明。

如图5所示,原始输入在经过Token Embedding后,又加入了一个常数位置信息的的Positional Embedding。在经过一次线性变换后便得到了图5左右边所示的结果。接下来,我们再交换序列的位置,并同时进行Positional Embedding观察其结果。
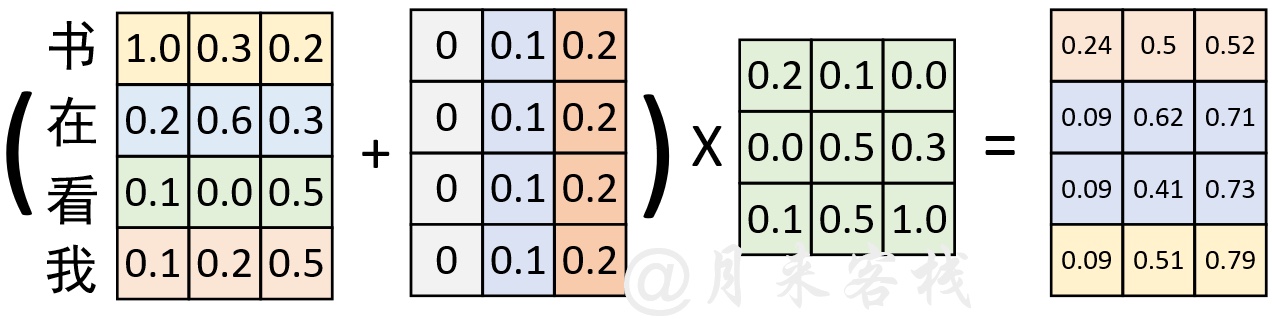
如图6所示,在交换序列位置后,采用同样的Positional Embedding进行处理,并且进行线性变换。可以发现,其计算结果同图5中的计算结果本质上也没有发生变换。因此,这就再次证明,如果Positional Embedding中位置信息是以常数形式进行变换,那么这样的Positional Embedding是无效的。
在Transformer中,作者采用了如公式所示的规则来生成各个维度的位置信息,其可视化结果如图4右所示。
其中就是这个Positional Embedding矩阵,表示具体的某一个位置,表示具体的某一维度。
最终,在融入这种非常数的Positional Embedding位置信息后,便可以得到如图7所示的对比结果。
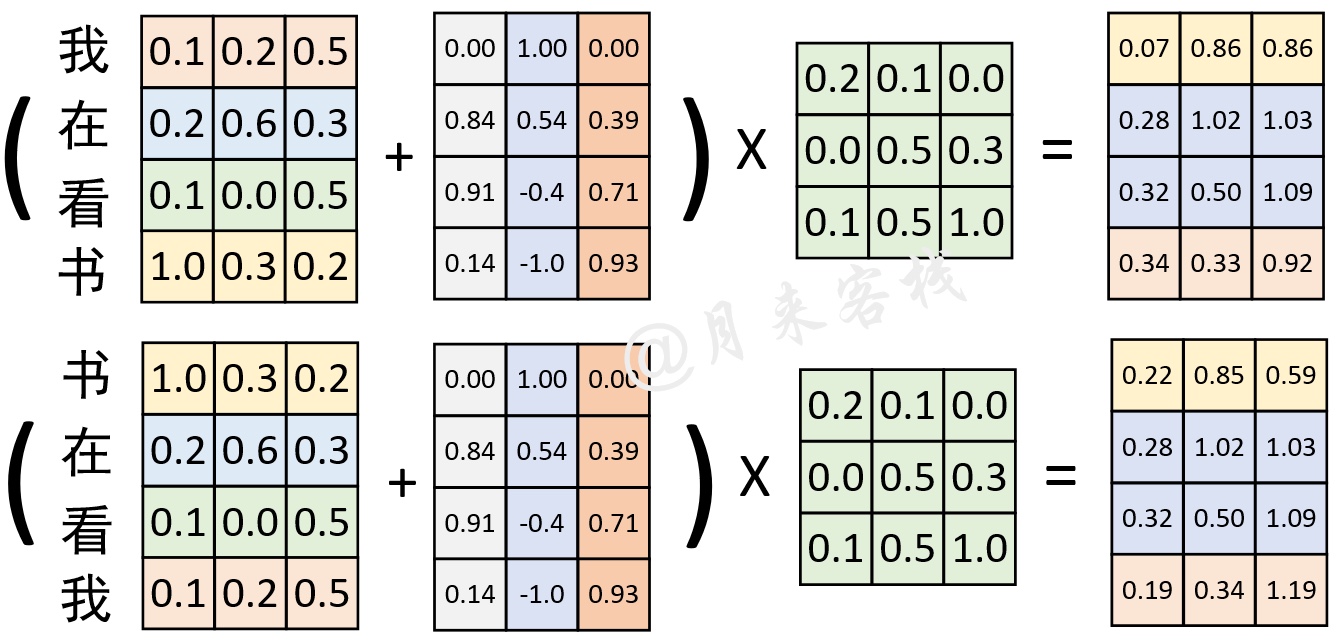
从图7可以看出,在交换位置前与交换位置后,与同一个权重矩阵进行线性变换后的结果截然不同。因此,这就证明通过Positional Embedding可以弥补自注意力机制不能捕捉序列时序信息的缺陷。
说完Transformer中的Embedding后,接下来我们再来继续探究Transformer的网络结构。
3 Transformer网络结构
如图8所示便是一个单层Transformer网络结构图。

如图8所示,整个Transformer网络包含左右两个部分,即Encoder和Decoder。下面,我们就分别来对其中的各个部分进行介绍。
3.1 Encoder层
首先,对于Encoder来说,其网络结构如图8所示(尽管论文中是以6个这样相同的模块堆叠而成,但这里我们先以堆叠一层来进行介绍,多层的Transformer结构将在稍后进行介绍)。
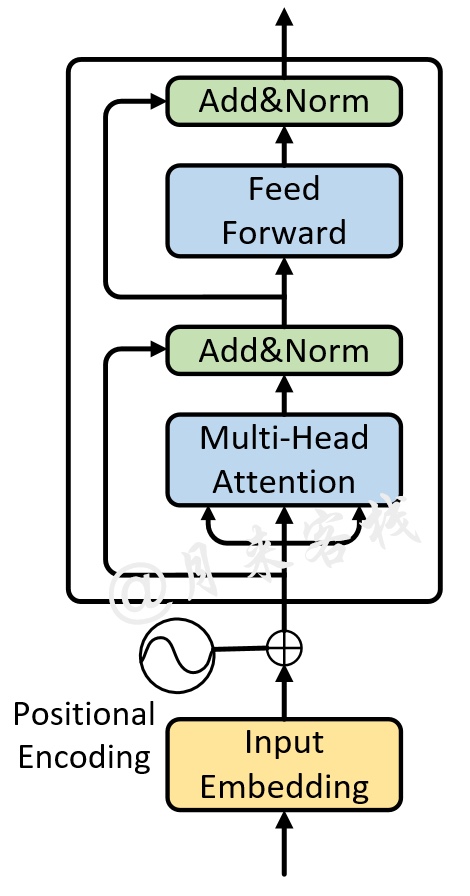
如图9所示,对于Encoder部分来说其内部主要由两部分网络所构成:多头注意力机制和两层前馈神经网络。
The encoder is composed of a stack of N = 6 identical layers. Each layer has two sub-layers. The first is a multi-head self-attention mechanism, and the second is a simple, position- wise fully connected feed-forward network.
同时,对于这两部分网络来说,都加入了残差连接,并且在残差连接后还进行了层归一化操作。这样,对于每个部分来说其输出均为,并且在都加入了Dropout操作。
We apply dropout to the output of each sub-layer, before it is added to the sub-layer input and normalized.
进一步,为了便于在这些地方使用残差连接,这两部分网络输出向量的维度均为。由于第1部分的多头注意力机制在上一篇文章中已经介绍过,在这里就不再赘述。
对于第2部分的两层全连接网络来说,其具体计算过程为
其中输入的维度为,第1层全连接层的输出维度为,第2层全连接层的输出为,且同时对于第1层网络的输出还运用了Relu激活函数。
到此,对于单层Encoder的网络结构就算是介绍完了,接下来让我们继续探究Decoder部分的网络结构。
3.2 Decoder层
同Encoder部分一样,论文中也采用了6个完全相同的网络层堆叠而成,不过这里我们依旧只是先看1层时的情况。对于Decoder部分来说,其整体上与Encoder类似,只是多了一个用于与Encoder输出进行交互的多头注意力机制,如图10所示。
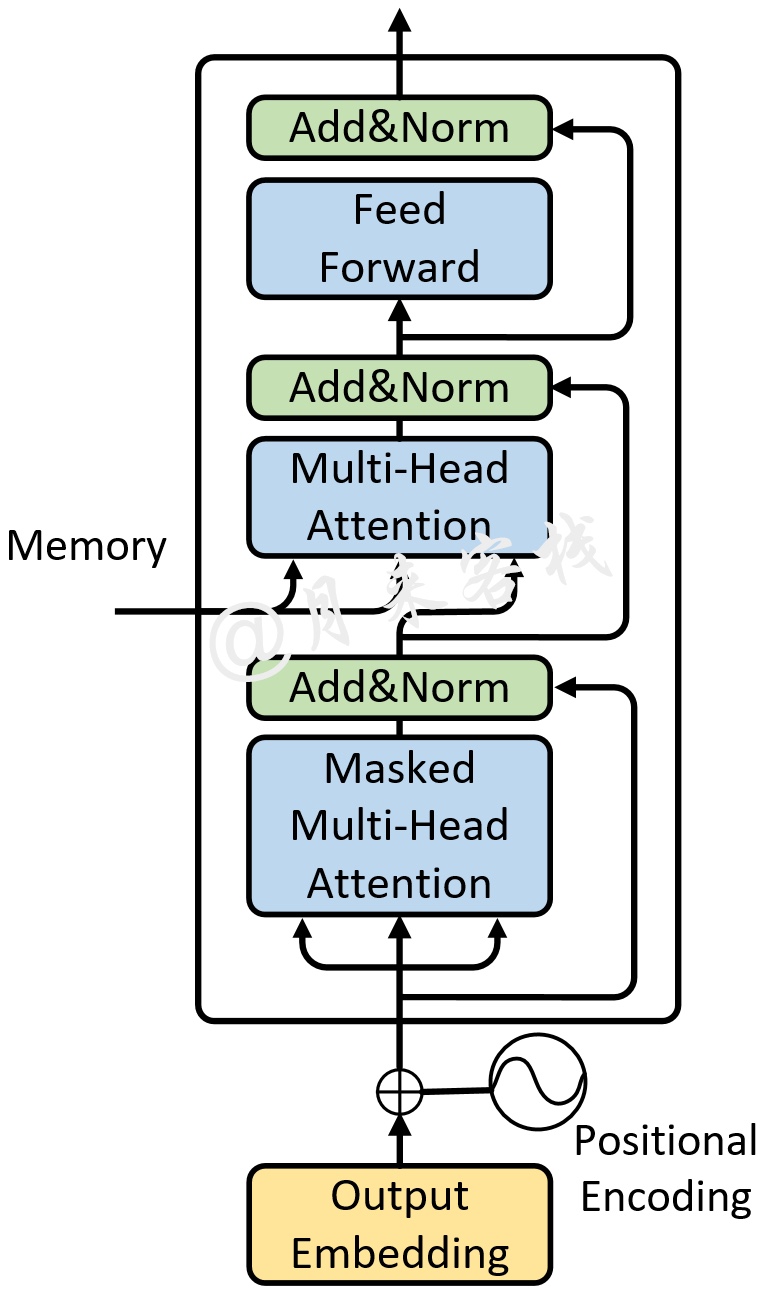
不同于Encoder部分,在Decoder中一共包含有3个部分的网络结构。最上面的和最下面的部分(暂时忽略Mask)与Encoder相同,只是多了中间这个与Encoder输出(Memory)进行交互的部分,作者称之为”Encoder-Decoder attention“。对于这部分的输入,Q来自于下面多头注意力机制的输出,K和V均是Encoder部分的输出(Memory)经过线性变换后得到。而作者之所以这样设计也是在模仿传统Encoder-Decoder网络模型的解码过程。
In "encoder-decoder attention" layers, the queries come from the previous decoder layer, and the memory keys and values come from the output of the encoder. This mimics the typical encoder-decoder attention mechanisms in sequence-to-sequence models
为了能够更好的理解这里Q、K、V的含义,我们先来看看传统的基于Encoder-Decoder的Seq2Seq翻译模型是如何进行解码的,如图10所示。
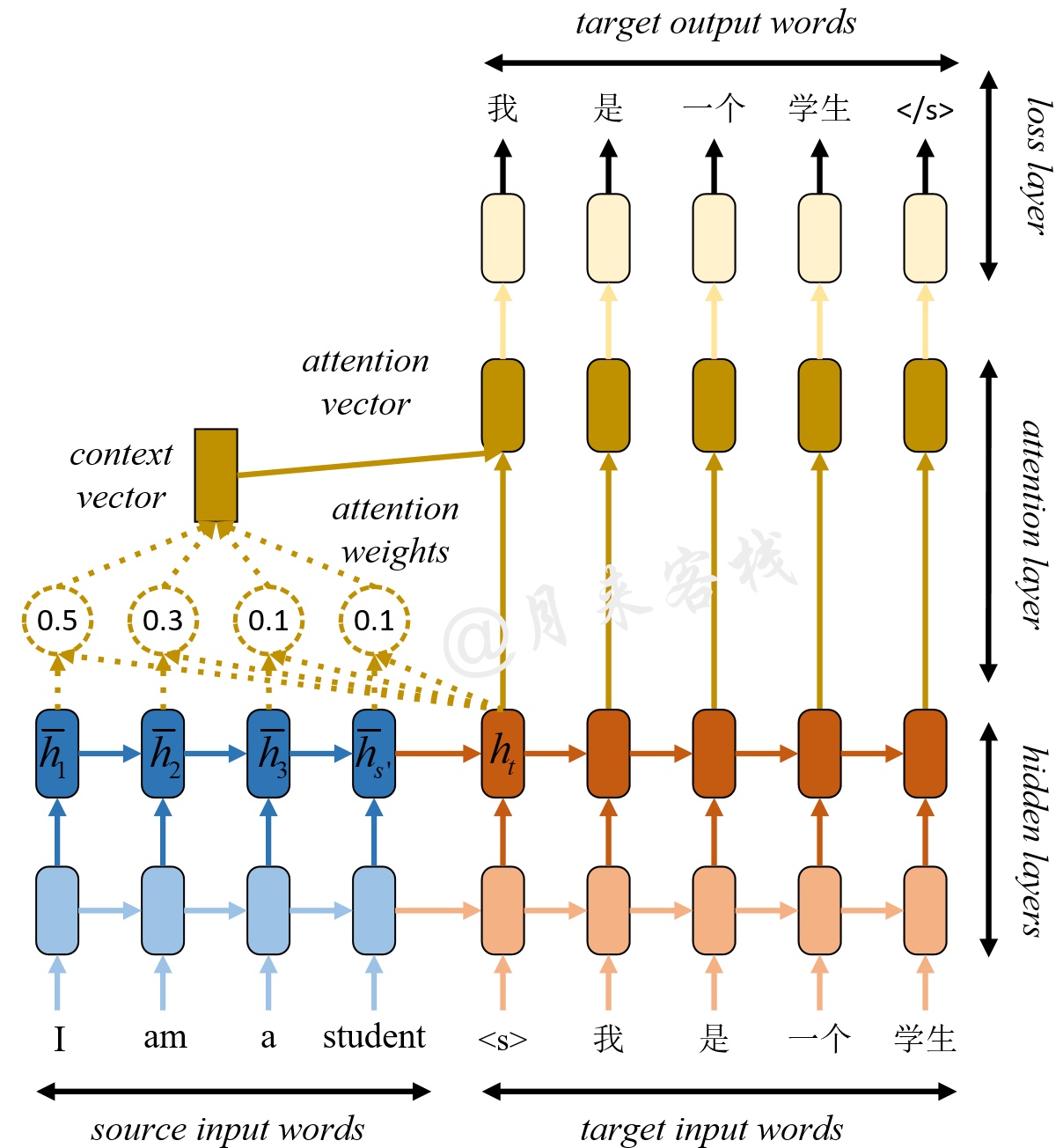
如图11所示是一个经典的基于Encoder-Decoder的机器翻译模型。左下边部分为编码器,右下边部分为解码器,左上边部分便是注意力机制部分。在图10中,表示的是在编码过程中,各个时刻的隐含状态,称之为每个时刻的Memory;表示解码当前时刻时的隐含状态。此时注意力机制的思想在于,希望模型在解码的时刻能够参考编码阶段每个时刻的记忆。
因此,在解码第一个时刻”< s >“时,会首先同每个记忆状态进行相似度比较得到注意力权重。这个注意力权重所蕴含的意思就是,在解码第一个时刻时应该将的注意力放在编码第一个时刻的记忆上(其它的同理),最终通过加权求和得到4个Memory的权重和,即context vector。同理,在解码第二时刻"我"时,也会遵循上面的这一解码过程。可以看出,此时注意力机制扮演的就是能够使得Encoder与Decoder进行交互的角色。
回到Transformer的Encoder-Decoder attention中,K和V均是编码部分的输出Memory经过线性变换后的结果(此时的Memory中包含了原始输入序列每个位置的编码信息),而Q是解码部分多头注意力机制输出的隐含向量经过线性变换后的结果。在Decoder对每一个时刻进行解码时,首先需要做的便是通过Q与 K进行交互(query查询),并计算得到注意力权重矩阵;然后再通过注意力权重与V进行计算得到一个权重向量,该权重向量所表示的含义就是在解码时如何将注意力分配到Memory的各个位置上。这一过程我们可以通过如图11和图12所示的过程来进行表示。
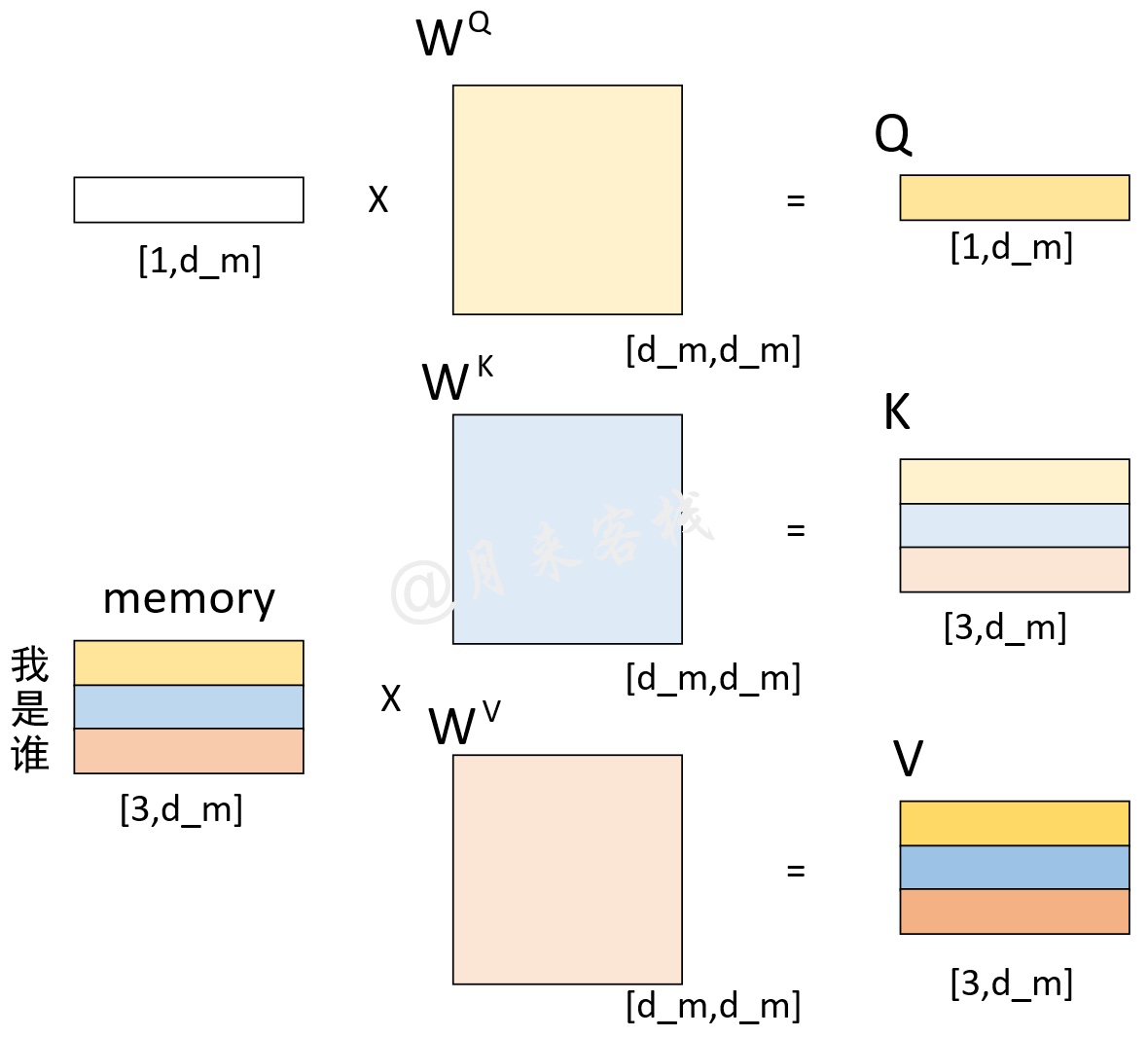
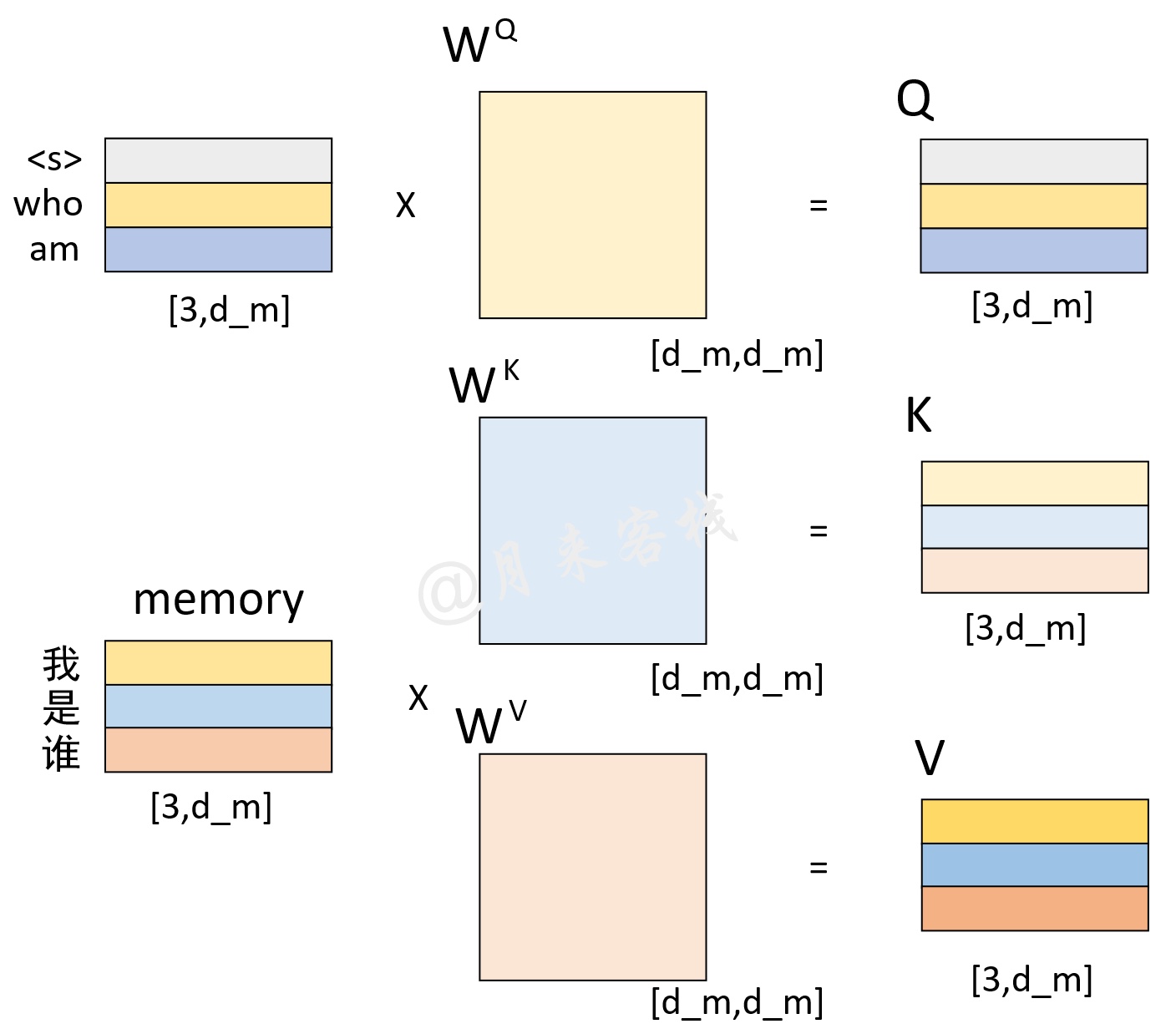
如图12所示,解码向量和Memory分别各自乘上一个矩阵后得到Q、K、V。
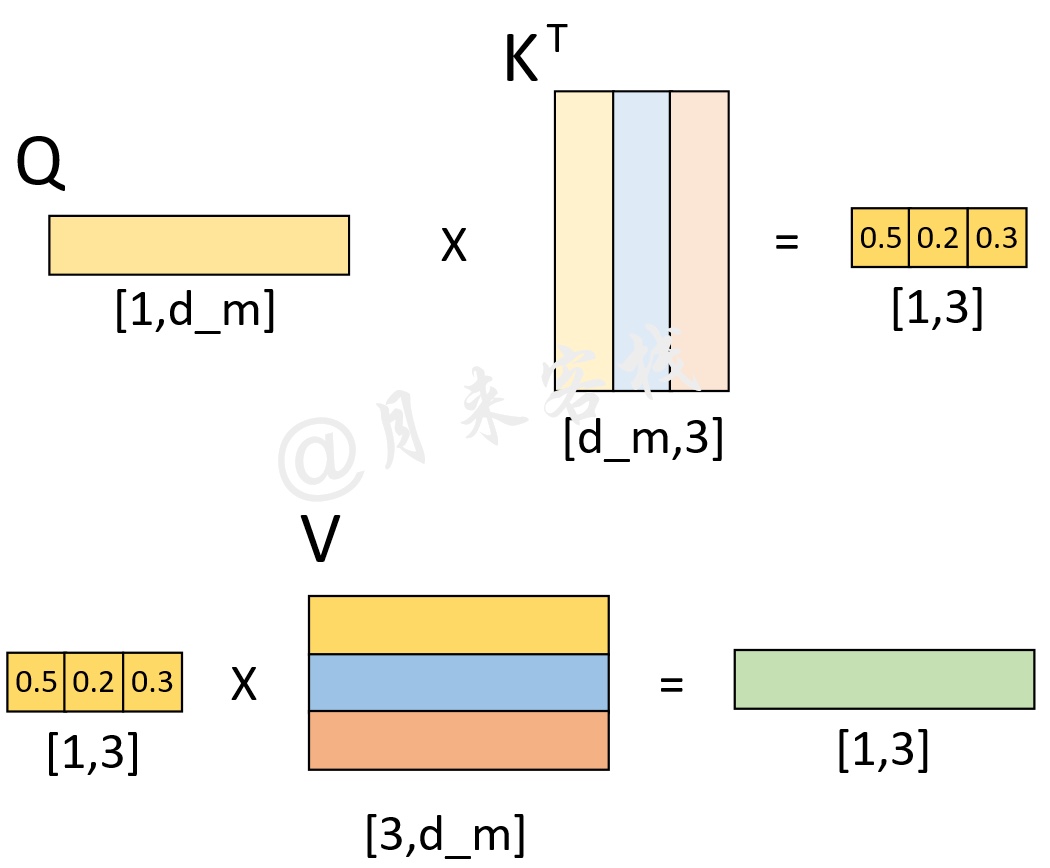
如图13所示,在解码第1个时刻时,首先Q通过与K进行交互得到权重向量,此时可以看做是Q(待解码向量)在K(本质上也就是Memory)中查询Memory中各个位置与Q有关的信息;然后将权重向量与V进行运算得到解码向量,此时这个解码向量可以看作是考虑了Memory中各个位置编码信息的输出向量,也就是说它包含了在解码当前时刻时应该将注意力放在Memory中哪些位置上的信息。
进一步,在得到这个解码向量并经过图10中最上面的两层全连接层后,便将其输入到分类层中进行分类得到当前时刻的解码输出值。
3.3 Decoder预测解码过程
当第1个时刻的解码过程完成之后,解码器便会将解码第1个时刻时的输入,以及解码第1个时刻后的输出均作为解码器的输入来解码预测第2个时刻的输出。整个过程可以通过如图14所示的过程来进行表示。
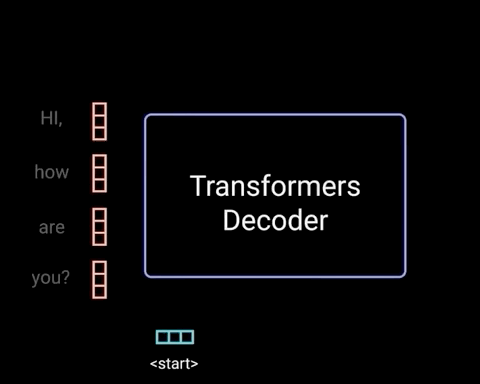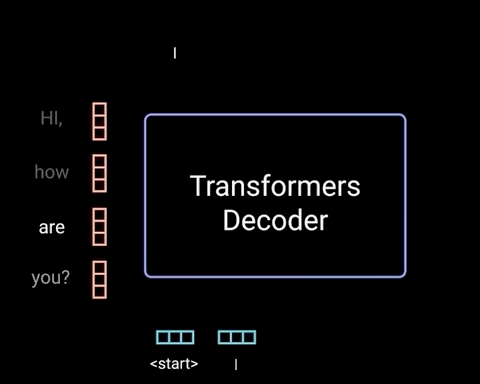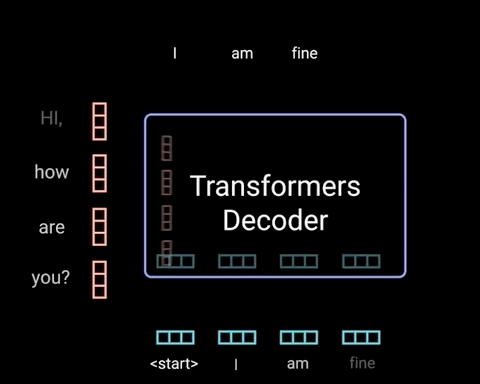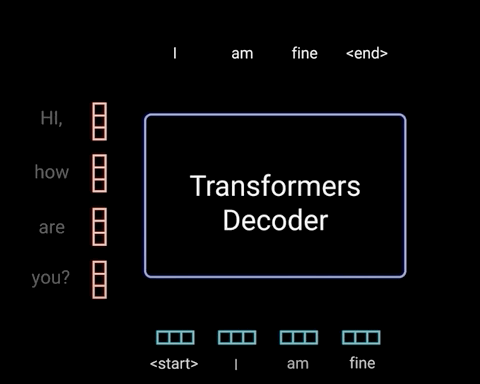
如图14所示,Decoder在对当前时刻进行解码输出时,都会将当前时刻之前所有的预测结果作为输入来对下一个时刻的输出进行预测。假设现在需要将”我 是 谁“翻译成英语”who am i“,且解码预测后前两个时刻的结果为"who am ",接下来需要对下一时刻的输出”i"进行预测,那么整个过程就可以通过图15和图16来进行表示。
如图15所示,左上角的矩阵是解码器对输入"< s > who am"这3个词经过多头注意力机制编码后的结果;左下角依旧是编码器读输入”我 是 谁“这3个词编码后的结果(同图12中的一样);两者分别在经过线性变换后便得到了Q、K和V这3个矩阵。此时值得注意的是,左上角矩阵中的每一个向量在经过多头注意力机制编码后,每个向量同样也包含了其它位置上的编码信息。
进一步,Q与K作用和便得到了一个权重矩阵;再将其与V进行线性组合便得到了Encoder-Decoder attention部分的输出,如图16所示。
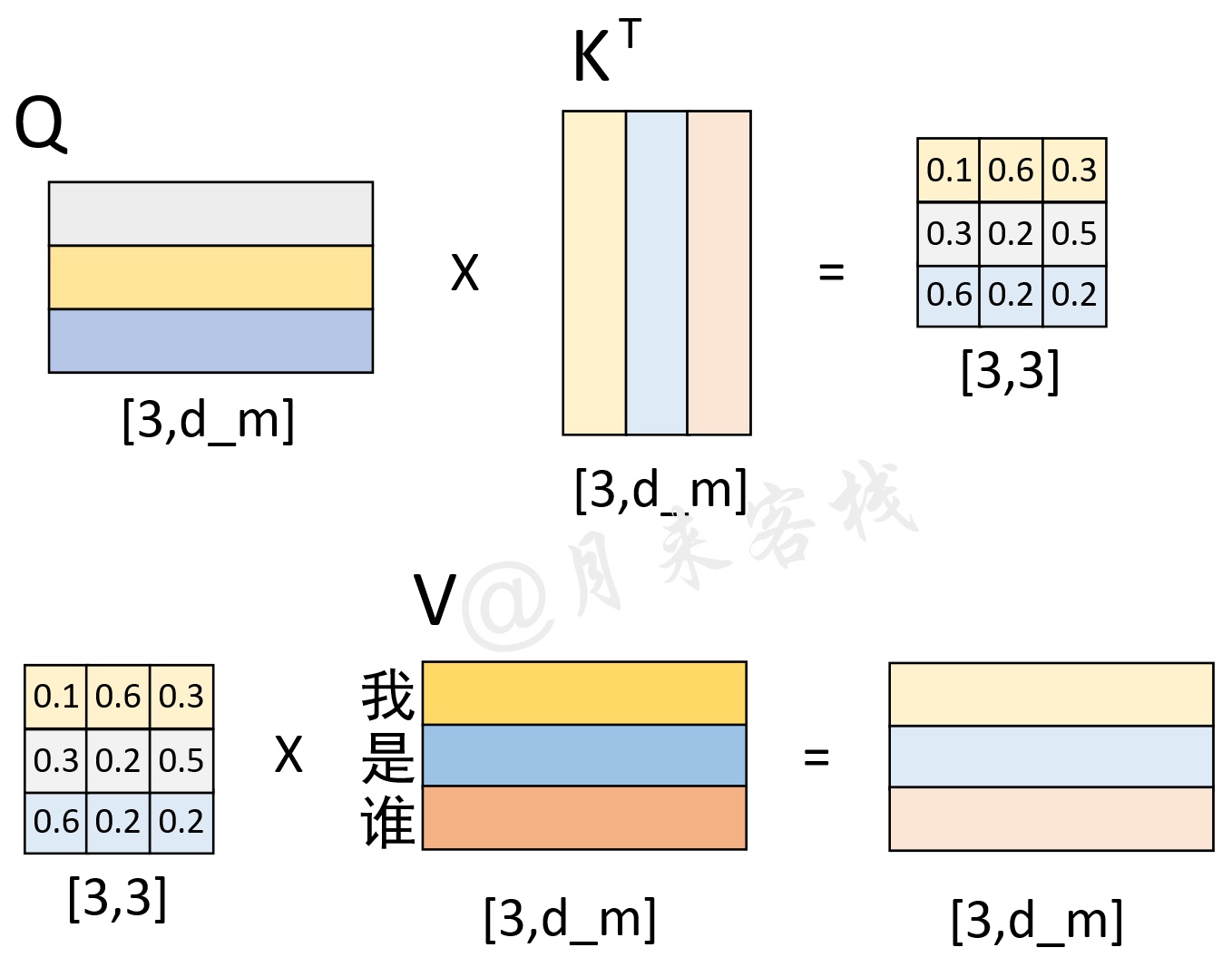
如图16所示,左下角便是Q与K作用后的权重矩阵,它的每一行就表示在对Memory(这里指V)中的每一位置进行解码时,应该如何对注意力进行分配。例如第3行的含义就是在解码当前时刻时应该将的注意力放在Memory中的"我"上,其它同理。这样,在经过解码器中的两个全连接层后,便得到了解码器最终的输出结果。接着,解码器会循环对下一个时刻的输出进行解码预测,知道预测结果为"< e >"或者达到指定长度后停止。
同时,这里需要注意的是,在通过模型进行实际的预测时,只会取解码器输出的其中一个向量进行分类,然后作为当前时刻的解码输出。例如图15中解码器最终会输出一个形状为[3,tgt_vocab_len]的矩阵,那么只会取其最后一个向量喂入到分类器中进行分类得到当前时刻的解码输出。具体细节见后续代码实现。
3.4 Decoder训练解码过程
在介绍完预测时Decoder的解码过程后,下面就继续来看在网络在训练过程中是如何进行解码的。从2.3小节的内容可以看出,在真实预测时解码器需要将上一个时刻的输出作为下一个时刻解码的输入,然后一个时刻一个时刻的进行解码操作。显然,如果训练时也采用同样的方法那将是十分费时的。因此,在训练过程中,解码器也同编码器一样,一次接收解码时所有时刻的输入进行计算。这样做的好处,一是通过多样本并行计算能够加快网络的训练速度;二是在训练过程中直接喂入解码器正确的结果而不是上一时刻的预测值能够更好的训练网络。
例如在用平行预料”我 是 谁“<==>”< s > who am i < e >“对网络进行训练时,编码器的输入便是”我 是 谁“,而解码器的输入则是”< e > who am i < e>“。
假设现在解码器的输入”< s > who am i < e >“在分别乘上一个矩阵进行线性变换后得到了Q、K、V,且Q与K作用后得到了注意力权重矩阵(此时还未进行softmax操作),如图17所示。
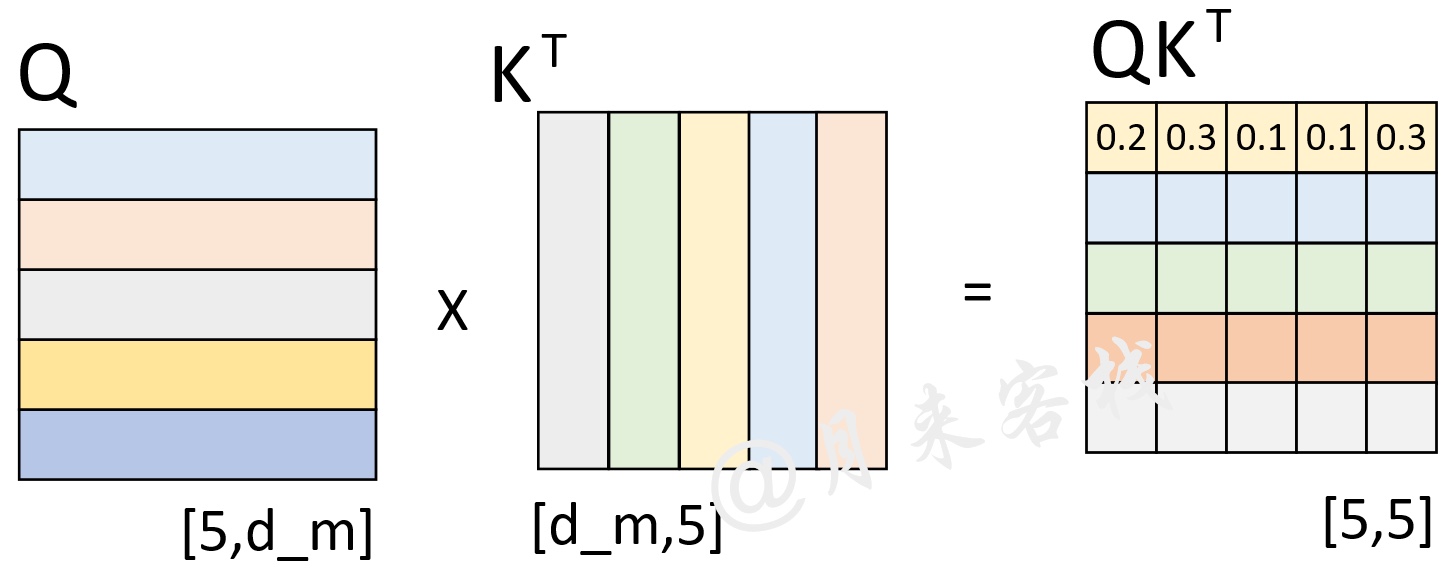
从图16可以看出,此时已经计算得到了注意力权重矩阵。由第1行的权重向量可知,在解码第1个时刻时应该将(严格来说应该是经过softmax后的值)的注意力放到'< s >'上,的注意力放到'who'上等等。不过此时有一个问题就是,在2.3节中笔者介绍到,模型在实际的预测过程中只是将当前时刻之前(包括当前时刻)的所有时刻作为输入来预测下一个时刻,也就是说模型在预测时是看不到当前时刻之后的信息。因此,Transformer中的Decoder通过加入注意力掩码机制来解决了这一问题。
self-attention layers in the decoder allow each position in the decoder to attend to all positions in the decoder up to and including that position. We need to prevent leftward information flow in the decoder to preserve the auto-regressive property. We implement this inside of scaled dot-product attention by masking out (setting to −∞) all values in the input of the softmax which correspond to illegal connections.
如图18所示,左边依旧是通过Q和K计算得到了注意力权重矩阵(此时还未进行softmax操作),而中间的就是所谓的注意力掩码矩阵,两者在相加之后再乘上矩阵V便得到了整个自注意力机制的输出,也就是图10中的Masked Multi-Head Attention。
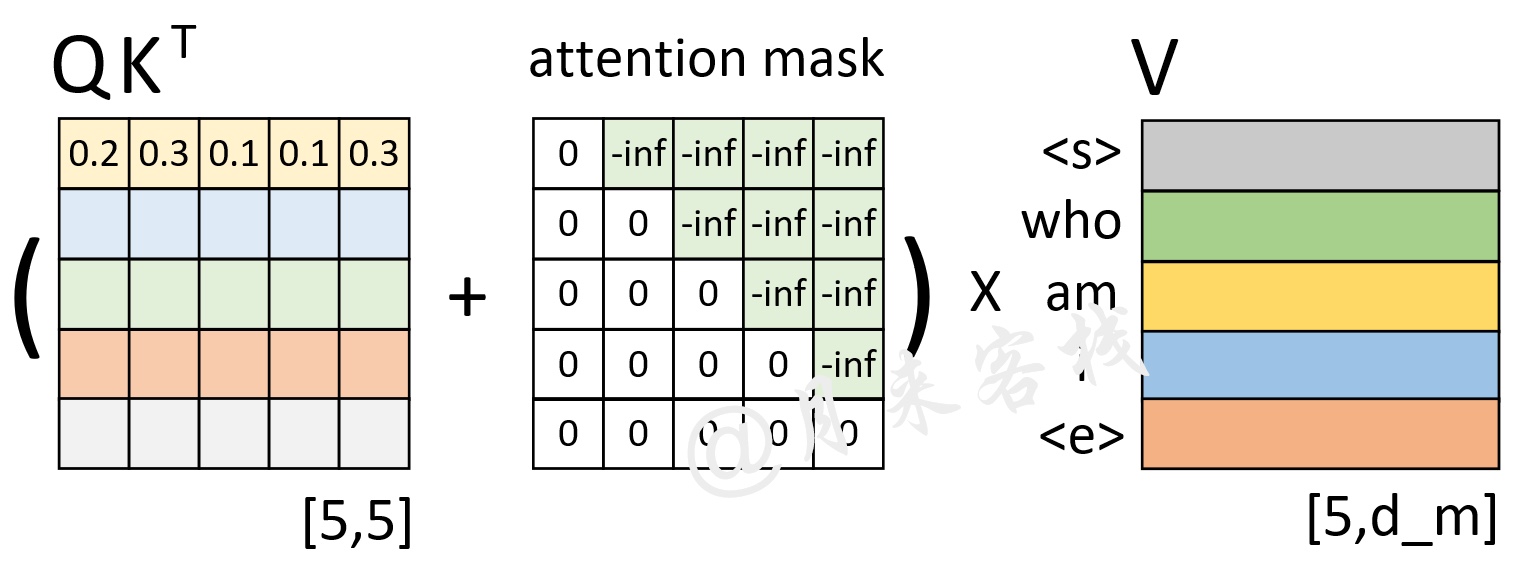
那为什么注意力权重矩阵加上这个注意力掩码矩阵就能够达到这样的效果呢?以图17中第1行权重为例,当解码器对第1个时刻进行解码时其对应的输入只有'< s >',因此这就意味着此时应该将所有的注意力放在第1个位置上,换句话说也就是第1个位置上的权重应该是1,而其它位置则是0。从图17可以看出,第1行注意力向量在加上第1行注意力掩码,再经过softmax操作后便得到了一个类似的向量。那么,通过这个向量就能够保证在解码第1个时刻时只能将注意力放在第1个位置上的特性。同理,在解码后续的时刻也是类似的过程。
到此,对于整个单层Transformer的网络结构以及编码解码过程就介绍完了,更多细节内容见后续代码实现。
4 总结
在本篇文章中,笔者首先介绍了Token Embedding和Positional Embedding,以及在Transformer中为什么需要使用Positional Embedding的原因;接着介绍了单层Transformer的整体网络结构,包括编码层、解码层、预测时的解码过程以及训练时的解码过程;最后详细介绍了什么是Masked Multi-Head Attention以及为什么需要使用它。在下一篇文章中,笔者将会介绍多层Transformer的网络结构以及多头注意力机制的实现过程。
本次内容就到此结束,感谢您的阅读!如果你觉得上述内容对你有所帮助,欢迎分享至一位你的朋友!若有任何疑问与建议,请添加笔者微信'nulls8'或加群进行交流。青山不改,绿水长流,我们月来客栈见!
引用
[1] This post is all you need(多头注意力机制原理)


