Transformers自定义学习了动态调整

1 引言

各位朋友大家好，欢迎来到月来客栈，我是掌柜空字符。

在深度学习模型的训练过程中，当训练出来的模型不那么尽如人意的时候相信大家第一时间想到的策略就是动态调整学习率。或者是在模型搭建的时候就想好了后面要通过动态调整学习率来训练模型。例如在Transformer论文中，作者就采用了如下公式来动态调整学习率：

lr_rate = d_{m o d e l}^{- 0.5} \cdot min ({step_num}^{- 0.5}, step_num \cdot {warmup_steps}^{- 1.5}) (1)

$(1)$ 的计算方式，模型在训练过程中学习率的变化便类似图1所示：

图 1. Transformer动态学习率变化图

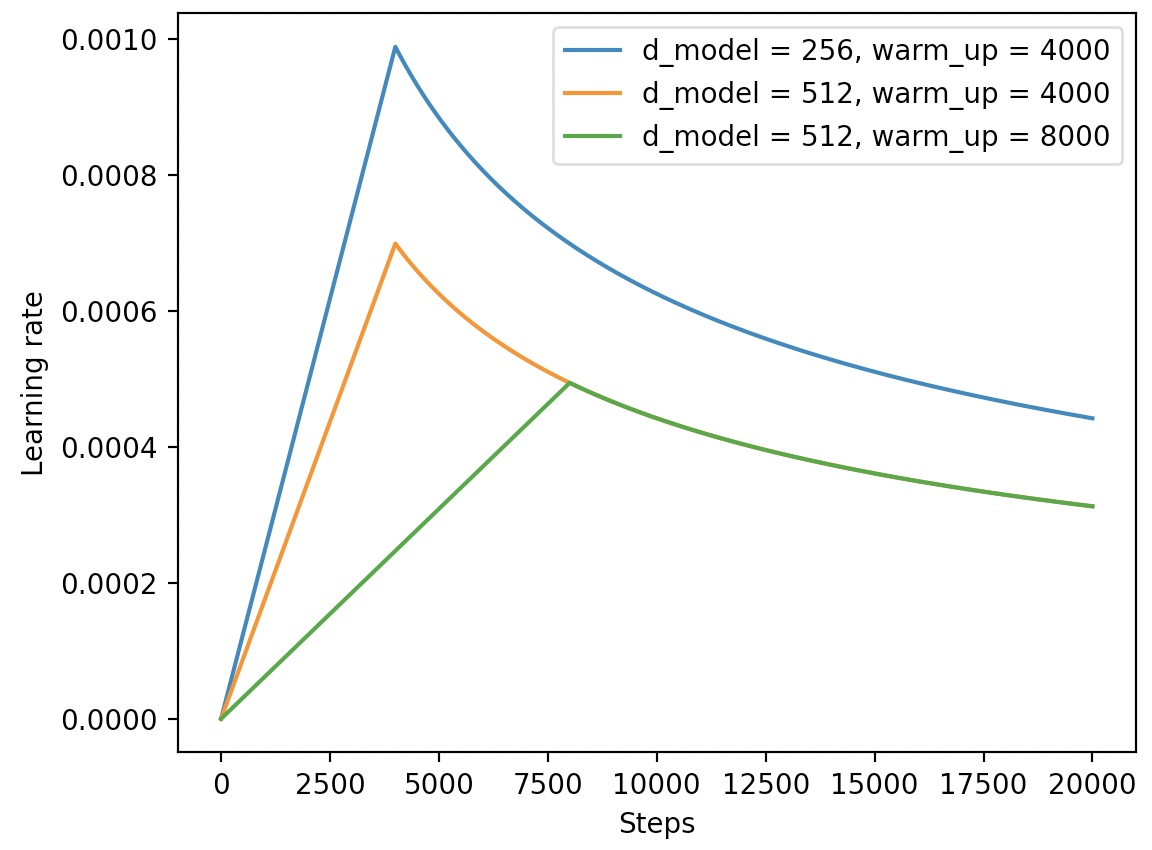
并且，我们还可以通过如下代码来实现模型学习率在训练过程中的动态调整：


xxxxxxxxxx
27
1
class CustomSchedule(object):
2
    def __init__(self, d_model, warmup_steps=4000, optimizer=None):
3
        super(CustomSchedule, self).__init__()
4
        self.d_model = torch.tensor(d_model, dtype=torch.float32)
5
        self.warmup_steps = warmup_steps
6
        self.steps = 1.
7
        self.optimizer = optimizer
8

9
    def step(self):
10
        arg1 = self.steps ** -0.5
11
        arg2 = self.steps * (self.warmup_steps ** -1.5)
12
        self.steps += 1.
13
        lr = (self.d_model ** -0.5) * min(arg1, arg2)
14
        for p in self.optimizer.param_groups:
15
            p['lr'] = lr
16
        return lr
17

18
def train(config):
19
    optimizer = torch.optim.Adam(translation_model.parameters(),
20
                                 lr=0.,
21
                                 betas=(config.beta1, config.beta2), eps=config.epsilon)
22
    lr_scheduler = CustomSchedule(config.d_model, optimizer=optimizer)
23
    ...
24
    loss.backward()
25
    lr_scheduler.step()
26
    optimizer.step()
27
    ...

在上述代码中，第1-16行是整个自定义学习率的实现部分，其中warmup_steps表示学习率在达到最大值前的一个”热身步数“（例如图1中的直线部分）；第25行则是在每个训练的step中对学习率进行更新；第26行则是采用更新后的学习率对模型参数进行更新。

当然，对于这类复杂或并不常见的学习率动态调整确实需要我们自己来编码实现，但是对于一些常见的常数、线性、余弦变换等学习率调整，我们可以直接借助Transformers框架中的optimization模块来实现。

在本篇文章中，掌柜将会先来介绍如何直接使用Transformers框架中的optimization模块来快速实现学习率动态调整的目的；然后再来简单介绍一下各个方法背后的实现逻辑以及如何模仿来实现自定义的方法。

2 学习率动态调整

在Transformers框架中，我们可以通过如下方式来导入optimization模块：


xxxxxxxxxx
1
1
from transformers import optimization

在optimization模块中，一共包含了6种常见的学习率动态调整方式，包括constant、constant_with_warmup、linear、polynomial、cosine 和cosine_with_restarts，其分别通过一个函数来返回对应的实例化对象。

下面掌柜就开始依次对这6种动态学习率调整方式进行介绍。

2.1 constant

在optimization模块中可以通过get_constant_schedule函数来返回对应的常数动态学习率调整方法。顾名思义，常数学习率动态调整就是学习率是一个恒定不变的常数，也就是说相当于没用。为了方便后续对学习率的变化进行可视化，这里我们先随便定义一个网络模型，代码如下：


xxxxxxxxxx
11
1
import torch
2
import torch.nn as nn
3

4
class Model(nn.Module):
5
    def __init__(self):
6
        super(Model, self).__init__()
7
        self.fc = nn.Linear(5, 10)
8

9
    def forward(self, x):
10
        out = self.fc(x).sum()
11
        return out

进一步，在模型训练的过程中，我们可以通过以下方式来进行使用：


xxxxxxxxxx
17
1
from transformers import optimization
2

3
if __name__ == '__main__':
4
    x = torch.rand([8, 5])
5
    model = Model()
6
    model.train()
7
    steps = 1000
8
    optimizer = torch.optim.Adam(model.parameters(), lr=1.0)
9
    scheduler = optimization.get_constant_schedule(optimizer, last_epoch=-1)
10
    lrs = []
11
    for _ in range(steps):
12
        loss = model(x)
13
        optimizer.zero_grad()
14
        loss.backward()
15
        optimizer.step()
16
        scheduler.step()
17
        lrs.append(scheduler.get_last_lr())

在上述代码中，第9行便是用来得到对应的常数学习率变化的实例化对象，其中last_epoch用于在恢复训练时指定上次结束时的epoch数量，因为有些方法学习率的变化会与epoch数有关，如果不考虑模型恢复的话指定为-1即可，这部分内容掌柜将在本文最后进行详细介绍；第16行则是对学习率进行更新；第17行则是取出对应的学习率便于可视化。

在模型训练结束后（或者采用tensorboard）便可以对学习率的变化进行可视化了，代码如下：


xxxxxxxxxx
4
1
    plt.figure(figsize=(7, 4))
2
    plt.plot(range(steps), lrs, label=name)
3
    plt.legend(fontsize=13)
4
    plt.show()

上述方法的可视化结果如下：

图 2. constant学习率变化图

如图2所示，模型在整个训练过程中的学习率并没有发生变化，都是保持着1.0的初始值。

2.2 constant_with_warmup

在optimization模块中可以通过get_constant_schedule_with_warmup函数来返回对应的动态学习率调整的实例化方法。从名字可以看出，该方法最终得到的是一个带warmup的常数学习率变化。在模型训练的过程中，我们可以通过以下方式来进行使用：


xxxxxxxxxx
1
1
scheduler = optimization.get_constant_schedule_with_warmup(optimizer, num_warmup_steps=300)

其中num_warmup_steps表示warmpup的数量。

最后，该方法的可视化结果如下所示：

图 3. constant_with_warmup学习率变化图

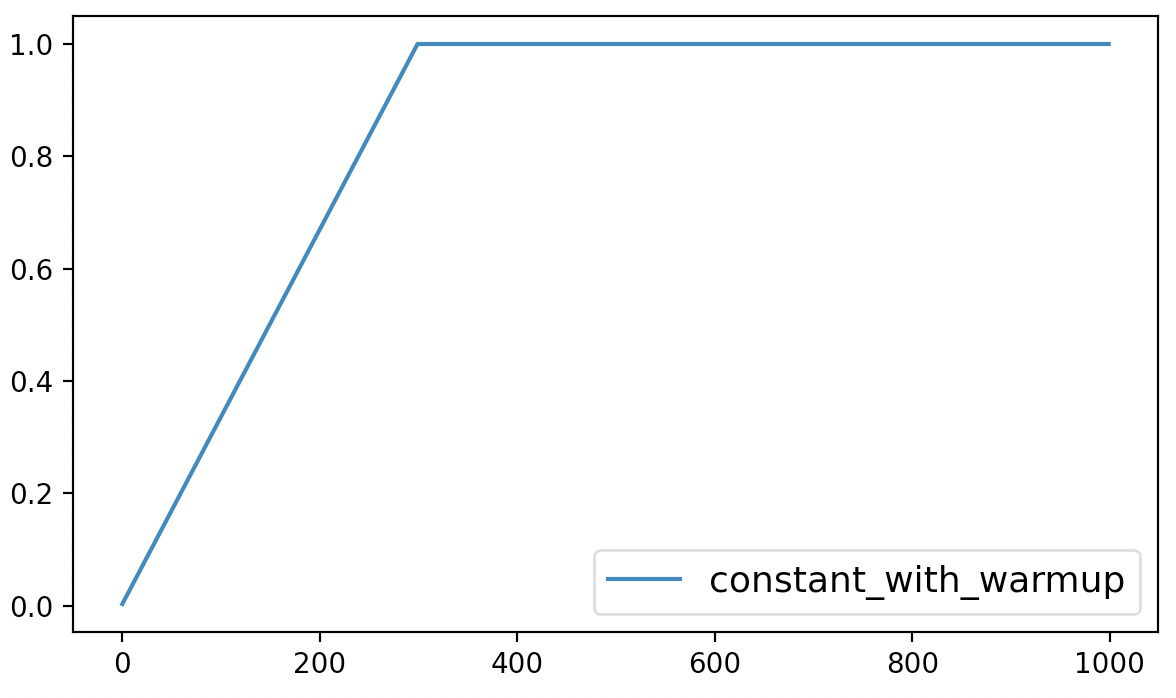
从图3可以看出constant_with_warmup仅仅只是在最初的300个steps中以线性的方式进行增长，之后便是同样保持为常数。

2.3 linear


xxxxxxxxxx
3
1
scheduler = optimization.get_linear_schedule_with_warmup(optimizer,
2
                                                         num_warmup_steps=300,
3
                                                         num_training_steps=steps)

其中num_training_steps表示整个模型训练的step数。

最后，该方法的可视化结果如下所示：

图 4. linear学习率变化图

从图4可以看出linear动态学习率调整先是在最初的300个steps中以线性的方式进行增长，之后便是同样以线性的方式进行递减，直到衰减到0为止。

2.4 polynomial

在optimization模块中可以通过get_constant_schedule_with_warmup函数来返回对应的动态学习率调整的实例化方法。从名字可以看出，该方法最终得到的是一个基于多项式的学习率动态调整策略。在模型训练的过程中，我们可以通过以下方式来进行使用：


xxxxxxxxxx
5
1
scheduler = optimization.get_polynomial_decay_schedule_with_warmup(optimizer,
2
                                                                   num_warmup_steps=300,
3
                                                                   num_training_steps=steps,
4
                                                                   lr_end = 1e-7,
5
                                                                   power=3)

其中power表示多项式的次数，当power=1时（默认）等价于get_linear_schedule_with_warmup函数；lr_end表示学习率衰减到的最小值。

最后，该方法的可视化结果如下所示：

图 5. polynomial学习率变化图（power=3）

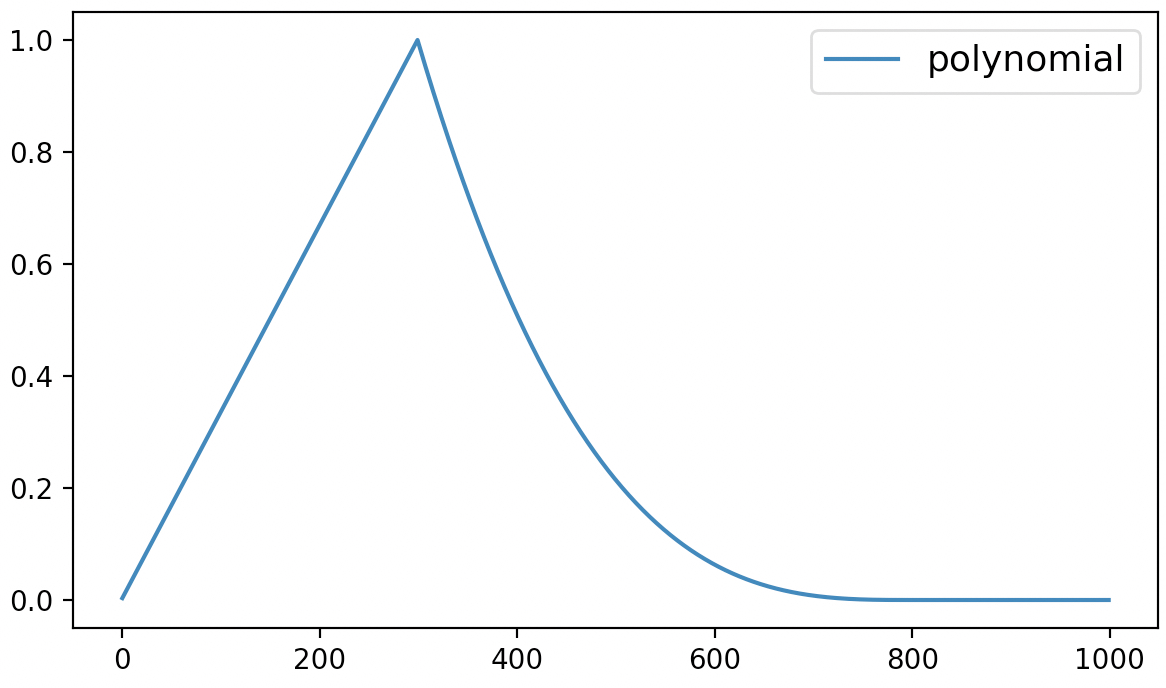
从图5可以看出polynomial动态学习率调整先是在最初的300个steps中以线性的方式进行增长，之后便是多项式的方式进行递减，直到衰减到lr_end后保持不变。

2.5 cosine

在optimization模块中可以通过get_cosine_schedule_with_warmup来返回基于cosine函数的动态学习率调整方法。在模型训练过程中我们可以通过如下方式来进行调用：


xxxxxxxxxx
4
1
scheduler = optimization.get_cosine_schedule_with_warmup(optimizer,
2
                                                         num_warmup_steps=300,
3
                                                         num_training_steps=steps,
4
                                                         num_cycles=2)

其中num_cycles表示循环的次数。

最后，该方法的可视化结果如下所示：

图 6. cosine学习率变化图（num_cycles=2）

从图6可以看出cosine动态学习率调整方法先是在最初的300个steps中以线性的方式进行增长，之后便是以余弦函数的方式进行周期性变换。

2.6 cosine_with_restarts

在optimization模块中可以通过get_cosine_with_hard_restarts_schedule_with_warmup来返回基于cosine函数的硬重启动态学习率调整方法。所谓硬重启就是学习率衰减到0之后直接变回到最大值的方式。在模型训练过程中我们可以通过如下方式来进行调用：


xxxxxxxxxx
4
1
scheduler = optimization.get_cosine_with_hard_restarts_schedule_with_warmup(optimizer,
2
                                                                            num_warmup_steps=300,
3
                                                                            num_training_steps=steps,
4
                                                                            num_cycles=2)

最后，该方法的可视化结果如下所示：

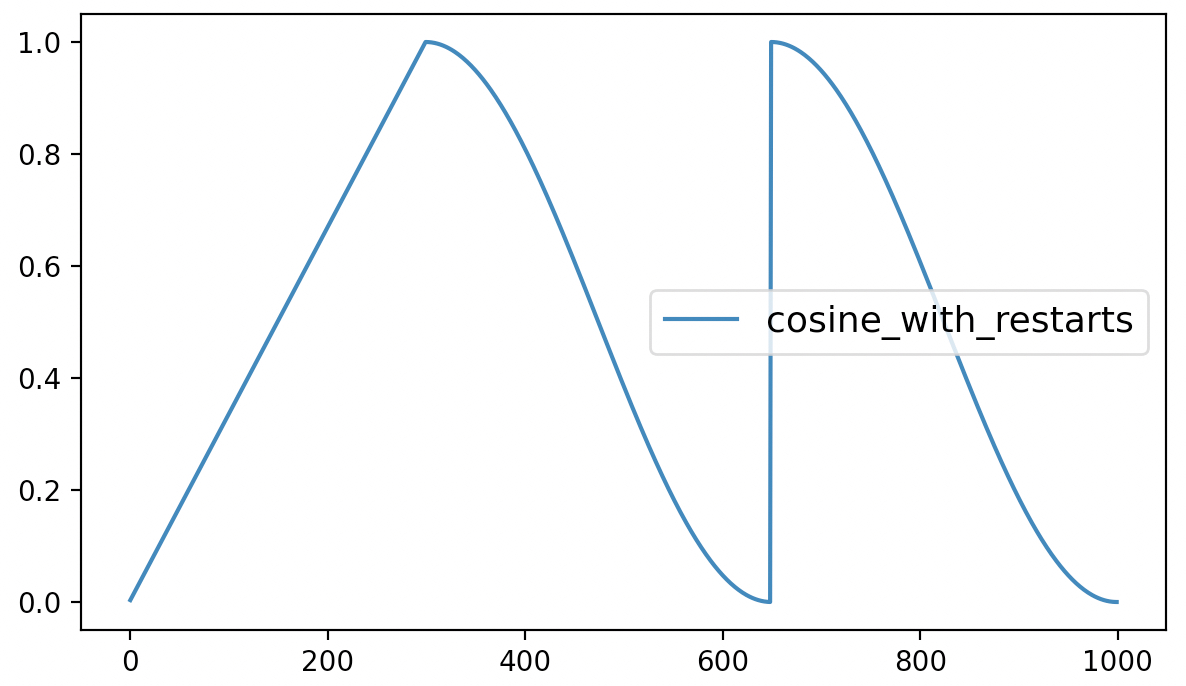
图 7. cosine_with_restarts学习率变化图（num_cycles=2）

从图7可以看出cosine_with_restarts动态学习率调整方法先是在最初的300个steps中以线性的方式进行增长，之后便是以余弦函数的方式进行周期性衰减，当达到最小值时再直接恢复到初始学习率。

2.7 get_scheduler

通过上述6个函数，我们便能够返回得到相应的动态学习率调整方法。当然，如果你并不需要修改一些特定的参数，例如多项式中的power和余弦变换中的num_cycles等，那么你还可以使用一个更加简单的统一接口来调用上述6个方法：


xxxxxxxxxx
6
1
from transformers import get_scheduler
2
def get_scheduler(
3
    name: Union[str, SchedulerType],
4
    optimizer: Optimizer,
5
    num_warmup_steps: Optional[int] = None,
6
    num_training_steps: Optional[int] = None):

在上述代码中，第3行name表示指定学习率调整的方式，可选项就是上面介绍的6种，并且通过constant、constant_with_warmup、linear、polynomial、cosine 和cosine_with_restarts这6个关键字就能够返回得到对应的方法；而对于其它特定的参数则会保持每个方法对应的默认值。例如通过get_scheduler函数返回get_cosine_with_hard_restarts_schedule_with_warmup时，num_cycles则为1

例如：


xxxxxxxxxx
6
1
scheduler = optimization.get_cosine_with_hard_restarts_schedule_with_warmup(optimizer,
2
                                                                            num_warmup_steps=300,
3
                                                                            num_training_steps=steps,
4
                                                                            num_cycles=1)
5
scheduler = get_scheduler(name="cosine_with_restarts", optimizer=optimizer,
6
                          num_warmup_steps=300, num_training_steps=steps)

在上述代码中，两种方式返回得到的学习调整方式都是一样的；但是如果想要返回num_cycles=2的情况那就不能通过get_scheduler函数获得。

到此，对于Transformes框架中常见的6种学习率动态调整方法及使用示例就介绍完了。

3 学习率调整实现

对于Transformers框架中实现的这6种学习率动态调整方法本质上也是基于PyTorch框架中的LambdaLR类而来。


xxxxxxxxxx
4
1
from torch.optim.lr_scheduler import LambdaLR
2
class LambdaLR(_LRScheduler):
3
    def __init__(self, optimizer, lr_lambda, last_epoch=-1):
4
        pass

通过这个接口，我们只需要指定优化器、学习率系数的计算方式（函数）以及last_epoch参数来实例化类LambdaLR便可以返回得到相应的实例化对象。下面掌柜就来依次进行一个简单的介绍。

3.1 constant实现

对于constant的计算过程来说比较简单，只需要传入一个返回值始终为1.0的匿名函数即可。因为返回的1将会作为一个系数乘以我们初始设定的学习率。实现代码如下：


xxxxxxxxxx
2
1
def get_constant_schedule(Optimizer, last_epoch = -1):
2
    return LambdaLR(optimizer, lambda _: 1, last_epoch=last_epoch)

在上述代码中，lambda _:1就是对应返回值为1的匿名函数。

3.2 constant_with_warmup实现

对于constant_with_warmup的计算过程来说同样也比较简单。整体逻辑便是在num_warmup_steps之前系数保持线性增长，在num_warmup_steps之后保持为1.0不变即可，即：

\begin{matrix} lr_coef = {\begin{cases} \frac{current_step}{num_warmup_steps}, & current_step < num_warmup_steps \\ 1.0, & current_step \geq num_warmup_steps \end{cases} (2) \end{matrix}

$(2)$ ，最终实现代码如下所示：


xxxxxxxxxx
6
1
def get_constant_schedule_with_warmup(Optimizer, num_warmup_steps,last_epoch = -1):
2
    def lr_lambda(current_step):
3
        if current_step < num_warmup_steps:
4
            return float(current_step) / float(max(1.0, num_warmup_steps))
5
        return 1.0
6
    return LambdaLR(optimizer, lr_lambda, last_epoch=last_epoch)

这里掌柜需要再次提醒大家的是，lr_lambda()返回的是学习率的变换系数，该系数乘以初始的学习率才是最终模型用到的学习率。例如上述代码中当current_step大于等于num_warmup_steps时返回的系数就是1，这样就能保证在这之后学习率就会保持初始设定的学习率不变。

3.3 linear实现

对于linear的系数计算过程来说只需要分别在num_warmup_steps之前和之后分别保持线性增加和线性减少即可，即：

\begin{matrix} lr_coef = {\begin{cases} \frac{current_step}{num_warmup_steps}, & current_step < num_warmup_steps \\ \frac{num_training_steps - current_step}{num_training_steps - num_warmup_steps}, & current_step \geq num_warmup_steps \end{cases} (3) \end{matrix}

$(3)$ ，最终实现代码如下所示：


xxxxxxxxxx
7
1
def get_linear_schedule_with_warmup(optimizer, num_warmup_steps, num_training_steps, last_epoch=-1):
2
    def lr_lambda(current_step: int):
3
        if current_step < num_warmup_steps:
4
            return float(current_step) / float(max(1, num_warmup_steps))
5
        return max( 0.0, float(num_training_steps - current_step) / 
6
          float(max(1, num_training_steps - num_warmup_steps)))
7
    return LambdaLR(optimizer, lr_lambda, last_epoch)

3.4 polynomial实现

对于polynomial的系数计算过程来说则稍微复杂了一点，其整体逻辑便是在num_warmup_steps之前系数保持线性增长，在num_warmup_steps之后保持为定值不变，在两者之间则以对应的多项式函数进行变换，计算公式式如下：

\begin{matrix} lr_coef = {\begin{cases} \frac{current_step}{num_warmup_steps}, & current_step < num_warmup_steps \\ \frac{lr_end}{lr_init}, & current_step > num_training_steps \\ \frac{(lr_init - lr_end) \cdot {[1 - \frac{current_step - num_warmup_steps}{num_training_steps - num_warmup_steps}]}^{power} + lr_end}{lr_init}, & num_warmup_steps \leq current_step \leq num_training_steps \end{cases} (4) \end{matrix}

$\text{lr\_init}$ 表示初始设定的学习率。

$(4)$ ，最终实现代码如下所示：


xxxxxxxxxx
16
1
def get_polynomial_decay_schedule_with_warmup(optimizer, 
2
            num_warmup_steps, num_training_steps, lr_end=1e-7, power=1.0, last_epoch=-1):
3
    lr_init = optimizer.defaults["lr"]
4
    assert lr_init > lr_end, f"lr_end ({lr_end}) must be be smaller than initial lr ({lr_init})"
5
    def lr_lambda(current_step):
6
        if current_step < num_warmup_steps:
7
            return float(current_step) / float(max(1, num_warmup_steps))
8
        elif current_step > num_training_steps:
9
            return lr_end / lr_init  # as LambdaLR multiplies by lr_init
10
        else:
11
            lr_range = lr_init - lr_end
12
            decay_steps = num_training_steps - num_warmup_steps
13
            pct_remaining = 1 - (current_step - num_warmup_steps) / decay_steps
14
            decay = lr_range * pct_remaining ** power + lr_end
15
            return decay / lr_init  # as LambdaLR multiplies by lr_init
16
    return LambdaLR(optimizer, lr_lambda, last_epoch)

3.5 cosine实现

对于cosine学习率动态变换的系数计算过程来说就稍微更复杂了，其整体逻辑便是在num_warmup_steps之前系数保持线性增长，在num_warmup_steps之后则以对应的余弦函数进行变换，计算公式如下：

\begin{matrix} lr_coef = {\begin{cases} \frac{current_step}{num_warmup_steps}, & current_step < num_warmup_steps \\ \frac{1}{2} \cdot (1 + \cos (2 \cdot π \cdot num_cycles \cdot \frac{current_step - num_warmup_steps}{num_training_steps - num_warmup_steps})), & current_step \geq num_warmup_steps \end{cases} (5) \end{matrix}

$(5)$ ，最终实现代码如下所示：


xxxxxxxxxx
9
1
def get_cosine_schedule_with_warmup(optimizer, num_warmup_steps,
2
                            num_training_steps, num_cycles = 0.5, last_epoch = -1):
3
    def lr_lambda(current_step):
4
        if current_step < num_warmup_steps:
5
            return float(current_step) / float(max(1, num_warmup_steps))
6
        progress = float(current_step - num_warmup_steps) / 
7
                   float(max(1, num_training_steps - num_warmup_steps))
8
        return max(0.0, 0.5 * (1.0 + math.cos(math.pi * float(num_cycles) * 2.0 * progress)))
9
    return LambdaLR(optimizer, lr_lambda, last_epoch)

3.6 cosine_with_restarts实现

对于cosine_with_restarts学习率动态变换的系数计算过程来说，总体上与cosine方式的实现过程类似，仅仅只是多增加了一个条件判断，具体计算公式如下：

\begin{matrix} lr_coef = {\begin{cases} \frac{current_step}{num_warmup_steps}, & current_step < num_warmup_steps \\ 0.0, & current_step > num_training_steps \\ \frac{1}{2} \cdot (1 + \cos (π \cdot (num_cycles \cdot \frac{current_step - num_warmup_steps}{num_training_steps - num_warmup_steps}) % 1.0)), & num_warmup_steps \leq current_step \leq num_training_steps \end{cases} (6) \end{matrix}

$\%$ 表示取余。

$(6)$ ，最终实现代码如下所示：


xxxxxxxxxx
11
1
def get_cosine_with_hard_restarts_schedule_with_warmup(optimizer, num_warmup_steps, 
2
                  num_training_steps, num_cycles = 1, last_epoch  = -1):
3
    def lr_lambda(current_step):
4
        if current_step < num_warmup_steps:
5
            return float(current_step) / float(max(1, num_warmup_steps))
6
        progress = float(current_step - num_warmup_steps) / 
7
                   float(max(1, num_training_steps - num_warmup_steps))
8
        if progress >= 1.0:
9
            return 0.0
10
        return max(0.0, 0.5 * (1.0 + math.cos(math.pi * ((float(num_cycles) * progress) % 1.0))))
11
    return LambdaLR(optimizer, lr_lambda, last_epoch)

3.7 transfromer实现

$(1)$ 也就是Transformer论文中学习率的调整，我们也可以模仿上述的方式来进行实现：


xxxxxxxxxx
8
1
def get_customized_schedule_with_warmup(optimizer, num_warmup_steps, d_model=1.0, last_epoch=-1):
2
    def lr_lambda(current_step):
3
        current_step += 1
4
        arg1 = current_step ** -0.5
5
        arg2 = current_step * (num_warmup_steps ** -1.5)
6
        return (d_model ** -0.5) * min(arg1, arg2)
7

8
    return LambdaLR(optimizer, lr_lambda, last_epoch)

$(1)$ 计算学习率的方法并不涉及到初始学习率的，所以在后面初始化Adam()时参数lr需要赋值为1.0，这样get_customized_schedule_with_warmup返回后的结果就直接是我们需要的学习率了。当然，也可以直接在上述代码第6行的返回值中再加上除以初始学习率，这样后续就不用有学习率必须设置为1的限制了，各位客官理解便是。

进一步我们就可以通过上述类似方式来使用该方法：


xxxxxxxxxx
4
1
optimizer = torch.optim.Adam(model.parameters(), lr=1.0)
2
scheduler = get_customized_schedule_with_warmup(optimizer,
3
                                                num_warmup_steps=200,
4
                                                d_model=728)

最终同样会得到如下图所示的学习率变化曲线：

图 8. 自定义学习率动态调整图

4 LambdaLR原理

在介绍完上述几种动态学习率调整及自定义的用法后，我们再来大致看看底层LambdaLR的实现逻辑，这样更有利于我们灵活的使用上述方法。当然，如果有客官暂时只想停留在对上述6种方式的使用层面，那么后续内容可以先行略过，等有需要再来查阅。

4.1 实现逻辑

翻阅LambdaLR类的实现代码可以发现，类LambdaLR是继承自类_LRScheduler，两者之中各类的类方法和类成员变量如下：


xxxxxxxxxx
42
1
class _LRScheduler(object):
2

3
    def __init__(self, optimizer, last_epoch=-1):
4
        if last_epoch == -1:
5
            for group in optimizer.param_groups:
6
                group.setdefault('initial_lr', group['lr'])
7
        ......
8
        self.base_lrs = list(map(lambda group: group['initial_lr'], optimizer.param_groups))
9
        self.last_epoch = last_epoch
10
        ......
11
        self.step()
12

13
    def get_lr(self):
14
        raise NotImplementedError
15

16
    def step(self, epoch=None):
17
        ......
18
        self._step_count += 1
19
        with _enable_get_lr_call(self):
20
            if epoch is None:
21
                self.last_epoch += 1
22
                values = self.get_lr()
23
            else:
24
                self.last_epoch = epoch
25
                if hasattr(self, "_get_closed_form_lr"):
26
                    values = self._get_closed_form_lr()
27
                else:
28
                    values = self.get_lr()
29
        for param_group, lr in zip(self.optimizer.param_groups, values):
30
            param_group['lr'] = lr
31
        ......
32

33
class LambdaLR(_LRScheduler):
34
  
35
    def __init__(self, optimizer, lr_lambda, last_epoch=-1):
36
        self.optimizer = optimizer
37
        self.last_epoch = last_epoch
38
        super(LambdaLR, self).__init__(optimizer, last_epoch)
39

40
    def get_lr(self):
41
        return [base_lr * lmbda(self.last_epoch)
42
                for lmbda, base_lr in zip(self.lr_lambdas, self.base_lrs)]

注意：上述代码并非完整部分，掌柜只是对其中的关键部分进行摘取。

要理解整个动态学习率的计算过程最重要的就是弄清楚get_lr()和step()这两个方法。从第3节中的使用示例可以发现，模型在训练过程中是通过step()这个方法来实现学习率更新的，因此这里我们就从step()方法入手来进行研究。

从上述代码第16行可以发现，其实step()方法在调用时还会接受一个epoch参数，但我们在前面的使用过程中并没有传入，那它又有什么用呢？进一步，从第20-22行可以当epoch为None时，那么self.last_epoch就会累计加1；而如果epoch不为None那么self.last_epoch就会直接取epoch的值；接着便是通过self.get_lr()函数来获取当前的学习率。在得到当前学习率的计算结果后，再通过第29-30行代码将其传入到优化器中便实现了学习率的动态调整。

接着我们再来看LambdaLR中get_lr()部分的实现代码。从第40-42行代码可知，self.lr_lambdas就是LambdaLR实例化时传入的参数lr_lambda，也就是第3节中介绍的学习率系数的计算函数；而self.last_epoch就是前面对应的current_step参数。从这里我们就可以发现，LambdaLR中epoch这个概念不仅仅有我们平常训练时所说的迭代“轮”数，也可以理解成训练时参数更新的次数。

从第20-28行的逻辑可以看出，如果在使用过程中需要学习率在每个batch参数更新时都发生变化，那么最简单的做法就是调用step()方法时不指定epoch；如果仅仅是需要在每个epoch（轮）后学习率才发生变化，那么在调用step()方法时指定epoch为当前的轮数即可，例如：


xxxxxxxxxx
4
1
for epoch in epoches:
2
    for data in data_iter:
3
        optimizer.step()
4
        scheduler.step(epoch=epoch)

通常来说，前一种方式（在每batch参数更新后学习率都发生改变）用到的时候更多，也就是第3节中介绍到的示例。

同时，根据上述代码第3-8行可知，当last_epoch=-1时，_LRScheduler就默认当前为模型刚开始训练时的状态，并把optimizer中的lr参数作为初始学习率initial_lr，也就是后续的self.base_lrs，就被用于在第42行中计算当前的学习率。当last_epoch不为-1时，也就意味着此时是的模型可能需要恢复到之前的某个时刻继续进行训练，那么学习率也就需要恢复到之前结束的那一刻。

到此，对于类LambdaLR的实现逻辑就算是基本介绍完了。下面掌柜再来介绍最后一个示例，即如何通过指定last_epoch来恢复到学习率之前的状态继续进行追加训练。

4.2 学习率恢复

假如某位客官正在采用cosine方法作为学习率动态调整策略来训练模型，并且在训练3个epoch后便结束了训练。同时也得到了如图9所示的学习率变化曲线：

图 9. 学习率变化曲线

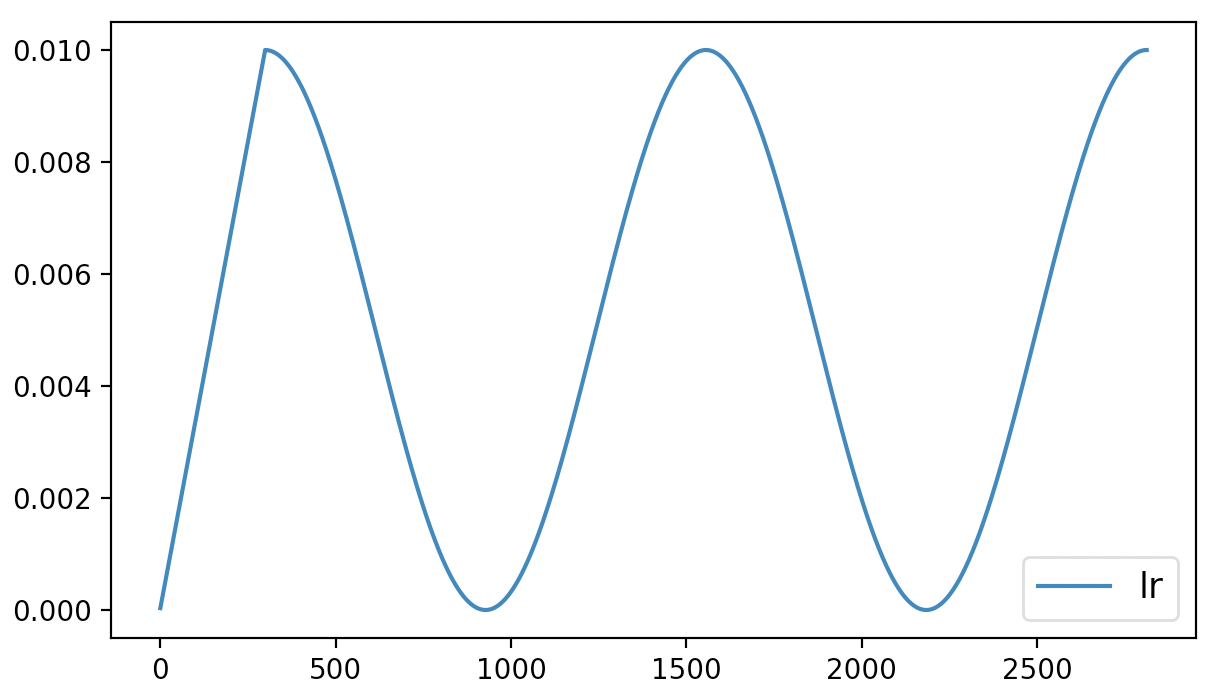
在这位客官认真分析完训练产生的相关数据后认为，模型如果继续进行训练应该还能获得更好的结果于是就打算对之前保存的模型进行追加训练。但是学习率要怎么样才能恢复到之前结束时的状态呢？也就是说模型在进行追加训练时学习率应该接着之前的状态继续进行，而不是像图9那样又从头开始。

此时，我们便可以通过如下代码来实现上述目的：


xxxxxxxxxx
24
1
        last_epoch = -1
2
        if os.path.exists('./model.pt'):
3
            checkpoint = torch.load('./model.pt')
4
            last_epoch = checkpoint['last_epoch']
5
            self.model.load_state_dict(checkpoint['model_state_dict'])
6

7
        num_training_steps = len(train_iter) * self.epochs
8
        optimizer = torch.optim.Adam([{"params": self.model.parameters(),
9
                                       "initial_lr": self.learning_rate}])
10
        scheduler = get_cosine_schedule_with_warmup(optimizer, num_warmup_steps=300,
11
                                                    num_training_steps=num_training_steps,
12
                                                    num_cycles=2, last_epoch=last_epoch)
13
        for epoch in range(self.epochs):
14
            for i, (x, y) in enumerate(train_iter):
15
                loss, logits = self.model(x, y)
16
                optimizer.zero_grad()
17
                loss.backward()
18
                optimizer.step()  # 执行梯度下降
19
                scheduler.step()
20
                lrs.append(scheduler.get_last_lr())
21
        ......
22
        torch.save({'last_epoch': scheduler.last_epoch,
23
                    'model_state_dict': self.model.state_dict()},
24
                   './model.pt')

在上述代码中，第2-5行用来判断本地是否存在模型，如果存在则获取对应的参数值；第7-12行则分别用来定义和实例化相关方法，当本地不存在模型时last_epoch将作为-1被传递到get_cosine_schedule_with_warmup中，即此时学习率从头开始变换；第22-24行则是对训练结束后的模型参数进行保存，同时也保存了last_epoch的值。

这里需要注意一点的是，只要在优化器中指定了initial_lr参数，那么LambdaLR在动态计算学习率时的base_lr就是initial_lr对应的值，与优化器中的指定的lr参数也就没有了关系。

当后续再对模型进行追加训练时，第4行代码便获取得到了last_epoch上一次训练结束后的值，接着后续训练时学习率就可以接着上一次结束时的状态继续进行。最终我们也可以得到如图10所示的学习率变化曲线：

图 10. 学习率变化曲线

从图10可以看出，学习率的初始值就是接着图9中学习率的结束值开始进行的变换。

5 总结

在本篇文章中，掌柜首先通过一个实例引出了什么是动态学习率调整；然后详细介绍了如何通过Transformers框架中的optimization模块来调用其实现的6种常见的动态学习率调整策略，并逐一进行了示例；接着介绍了PyTorch框架底层LambdaLR的实现逻辑，并对其中相关重要参数进行了讲解；最后通过一个示例介绍了如何在对模型进行追加训练时也能使得学习率恢复到之前训练时的状态。

本次内容就到此结束，感谢您的阅读！如果你觉得上述内容对你有所帮助，欢迎点赞转发分享三连！若有任何疑问与建议，请添加掌柜微信nulls8（备注来源）或加群进行交流。青山不改，绿水长流，我们月来客栈见！

引用

[1] 示例代码 https://github.com/moon-hotel/DeepLearningWithMe

Transformers自定义学习了动态调整

于2022年2月16日2022年2月16日由空字符发布

1 引言

2 学习率动态调整

2.1 constant

2.2 constant_with_warmup

2.3 linear

2.4 polynomial

2.5 cosine

2.6 cosine_with_restarts

2.7 get_scheduler

3 学习率调整实现

3.1 constant实现

3.2 constant_with_warmup实现

3.3 linear实现

3.4 polynomial实现

3.5 cosine实现

3.6 cosine_with_restarts实现

3.7 transfromer实现

4 LambdaLR原理

4.1 实现逻辑

4.2 学习率恢复

5 总结

引用

推荐阅读

Pytorch学习指南

基于BERT预训练模型的SQuAD问答任务

Pytorch学习指南

基于BERT预训练模型的SWAG问答任务

Pytorch学习指南

基于BERT预训练模型的英文文本蕴含任务

Transformers自定义学习了动态调整

于2022年2月16日2022年2月16日由 空字符 发布

1 引言

2 学习率动态调整

2.1 constant

2.2 constant_with_warmup

2.3 linear

2.4 polynomial

2.5 cosine

2.6 cosine_with_restarts

2.7 get_scheduler

3 学习率调整实现

3.1 constant实现

3.2 constant_with_warmup实现

3.3 linear实现

3.4 polynomial实现

3.5 cosine实现

3.6 cosine_with_restarts实现

3.7 transfromer实现

4 LambdaLR原理

4.1 实现逻辑

4.2 学习率恢复

5 总结

引用

推荐阅读

相关文章

Pytorch学习指南

基于BERT预训练模型的SQuAD问答任务

Pytorch学习指南

基于BERT预训练模型的SWAG问答任务

Pytorch学习指南

基于BERT预训练模型的英文文本蕴含任务

于2022年2月16日2022年2月16日由空字符发布