看不懂卷积或许只是因为

1 引言

通过前面一系列文章的介绍，我们算是对深度学习有了一个基本的概念，对于深层特征提取的重要性以及为什么要“深度”也应该有了一些清晰的认识。同时，我们也由逻辑回归和线性回归为基础延伸到了深度学习中的分类和回归模型，并且得出的一个结论就是，对于输出层之前的所有层，我们都可以将其看成是一个特征提取的过程，而且越靠后的隐含层也就意味着提取得到的特征越抽象。在得到这些抽象特征后，我们再通过最后一层来完成特定场景下的任务，这也就是深度学习的核心思想。由此，我们便可以将深度学习抽象成如下形式：

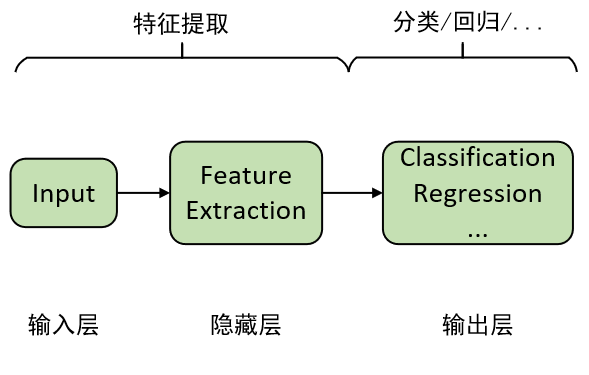
从图1中可以看到，对于深度学习来说，最重要最核心的部分当然就是隐藏层的特征提取过程。通过前面几篇文章的介绍，我们已经熟悉了通过深层前馈网络（也就是多个全连接层）来对输入进行特征提取。那说到这，还有没有其它进行特征提取的方式呢？有，当然有，而且还是百花齐放式的有，例如我们接下来就介绍到的卷积操作就是其中之一。所以，进一步，我们还可以用下面这个图来表示深度学习：

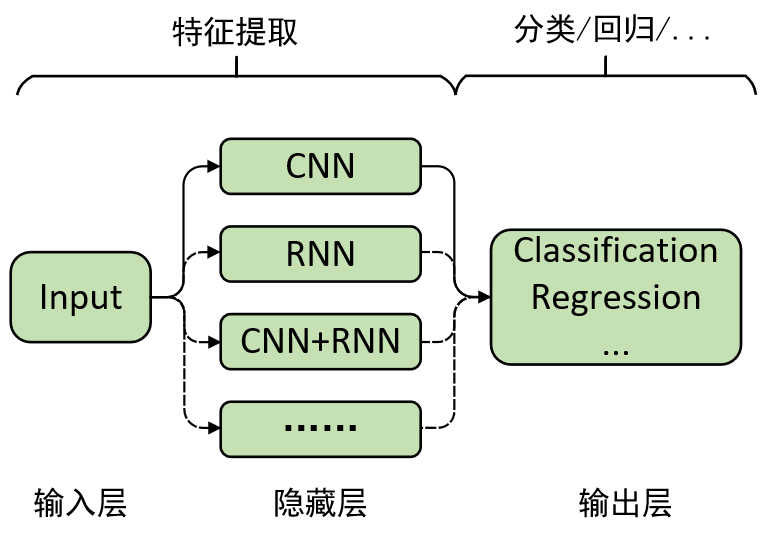
从图2中可以看出，我们可以通过不同的方式（技术）来对输入进行特征提取，然后再将提取得到的特征进行下一步的处理。因此，对于如何构造或者组合得到新的特征提取方式，也是深度学习中的一个重要研究方向。接下来，我们就开始对卷积操作进行介绍。

2 什么是卷积

卷积（convolutional ），它算得上是深度学习中最重要的技术之一了，其最早可以追溯到上世纪八十年代。直到今天，近四十年过去了，而这项技术依然是经久不衰的被用于各类网络模型中。说了这么多，那什么又是卷积呢？很多初学者看到在第一次知晓“卷积”这两个字后，总会陷入到数学概念中的那个卷积里来理解卷积，也就是通常会看到这么一句话来解释什么是卷积：卷积是通过两个函数$f$和$g$ 生成第三个函数的一种数学算子，表征函数$f$与$g$经过翻转和平移的重叠部分函数值乘积对重叠长度的积分[1]。

看完上面这句定义什么感受呢？是不是有种看了不如不看，甚至是还有点看了还“有害”的感觉？既然如此，那我们就从“卷积能够干什么”的角度来看看卷积到底是个什么鬼，并试着来揭开它的庐山真面目！

2.1 卷积能够干什么

首先需要清楚的是卷积操作也是用于对图像进行特征提取，并且还是主要用于图像处理领域中的一种技术。不过记性好的读者可能还记得我们在前面的一篇文章中介绍过如何用深层的全连接网络来对图像进行分类。简单点说就是先通过多层的全连接进行特征提取，然后最后通过softmax层来进行分类。那既然全连接网络也能对图片进行特征提取那我们为什么还需要卷积呢？两者有什么样的差异呢？

通常，以我们人类的思考问题的角度来看，对于任何一个用于图像分类的网络来说，其都应该满足如下几点特性：①平移不变性；②旋转不变性；③缩放不变性；④明暗不变性

• 平移不变性

  

  图 3. 平移不变性

  所谓平移不变性（Translation Invariance），指的是不管图片中的物体如何移动，网络总能够将其识别出来。

• 旋转不变性

  

  图 4. 旋转不变性

  所谓旋转不变性（Rotation Invariance），指的是不管图片中物体的角度如何变化，网络同样能够将其识别出来。

• 缩放不变性

  

  图 5. 缩放不变性

  所谓缩放不变性（Size Invariance），指的是不管图片中的物体被放大还是缩小，网络也能够将其识别出来。

• 明暗不变性

  

  图 6. 明暗不变性

  所谓明暗不变性（Illumination Invariance），指的是不管图片中物体的明暗程度如何变化，网络都能够将其识别出来。

  以上图片来自[2]

可以看出，对于上述这四点特性也非常符合我们观察事物的直觉。因此，对于图像识别模型来说，总不能因为位置或者角度变了就不能识别对吧。那什么样的特征提取方式能够同时满足这四项特性呢？

2.2 卷积的原理

为了回答上面这个问题，下面我们就来对全连接和卷积操作进行一个比较，看看它们俩在工作原理上有何不同。下面我们以在大小为4×4的图片中识别是否有下图所示的“横折”为例进行介绍。

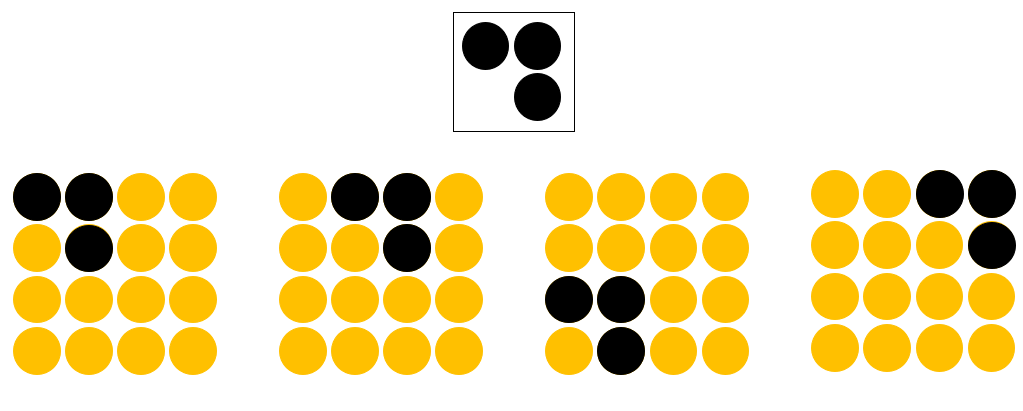
2.2.1 全连接网络识别“横折”

如图8所示为我们所采用的全连接网络结构图，其中输入层输入的是由图片拉伸后的向量。

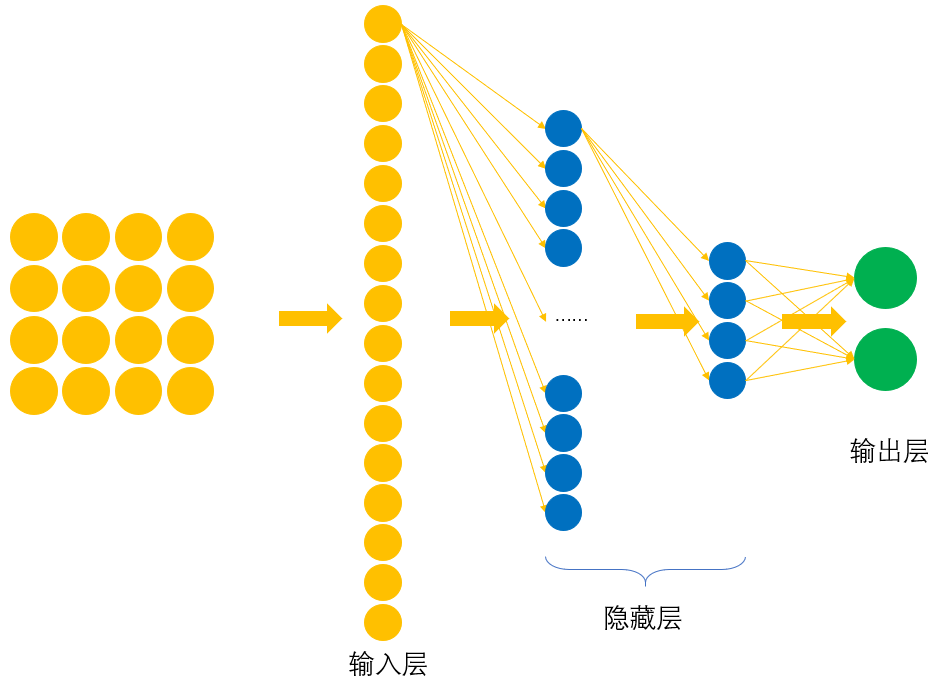
为了方便叙述，我们将输入层的神经元进行一个编号，如图9所示。

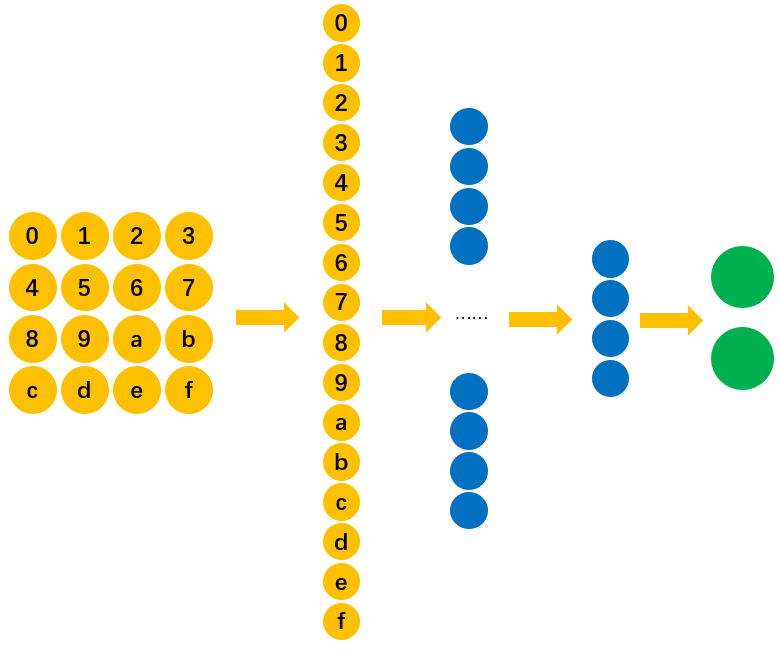
在有了网络结构后，我们仅用如下图10所示的训练集对网络进行进行训练即可。

现在问题来了，如果我们用通过图10中的训练集训练好的网络（网络A）来识别图11中的测试样本是否含有“横折”，那网络A能否成功识别呢？

遗憾的是，对于网络A来说只能是“臣妾做不到”。想想这是为什么呢？

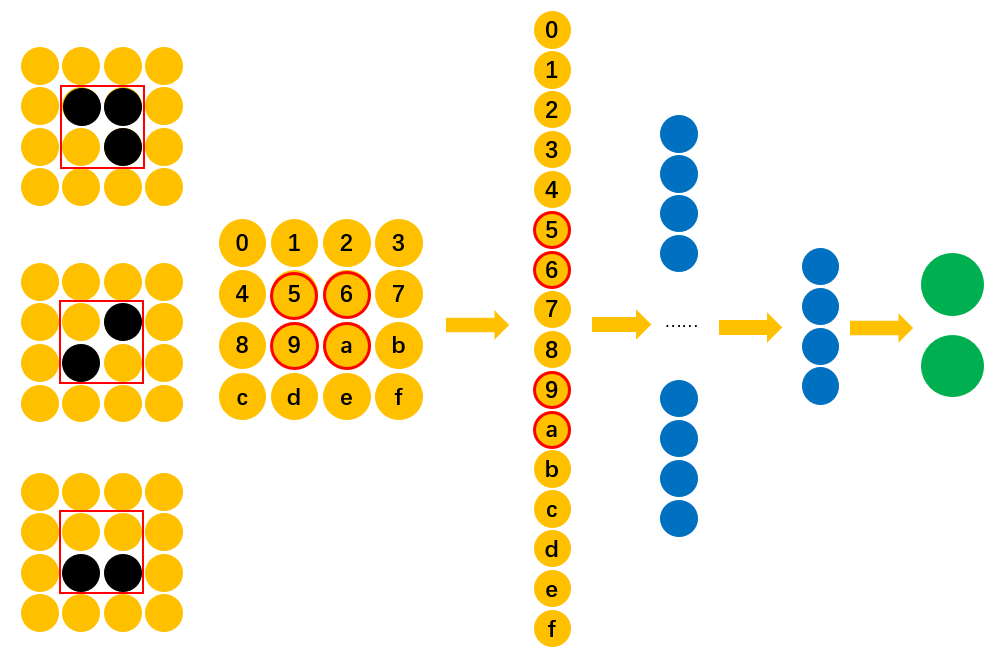
从图12中可以看到，由于在训练样本中，“横折”相关的信息仅仅只是分布在"5,6,9,a"这四个位置上，因此这也就意味着最终只有这四个位置对应的权重参数才对识别"5,6,9,a"中是否包含有“横折”有效。换句话说，只有"5,6,9,a"这四个位置对应的权重参数才是有效的。那怎么来解决这一问题，使得其它位置的权重参数同样有效，也能够识别“横折”呢？

对于解决这个问题，理论上至少会有两个办法：①用大量位于不同位置的“横折”数据对网络进行训练；②增加隐藏层的深度来提取得到更加抽象和高级的特征。但这样做的后果显然就是训练耗时，需要事先准备大量的训练集等。

我想，此时可能就有朋友不禁会问道，大家同样都是“横折”，为什么换个位置网络就不认识了？有没有什么方法可以将中间所学到的规律也运用在其他的位置？答案是有，让不同位置共享同样的权重即可，而这也就是卷积操作的核心思想。

2.2.2 卷积识别“横折”

上面说完了全连接网络是如何识别“横折”的，我们接下来看看卷积是网络是如何做的。

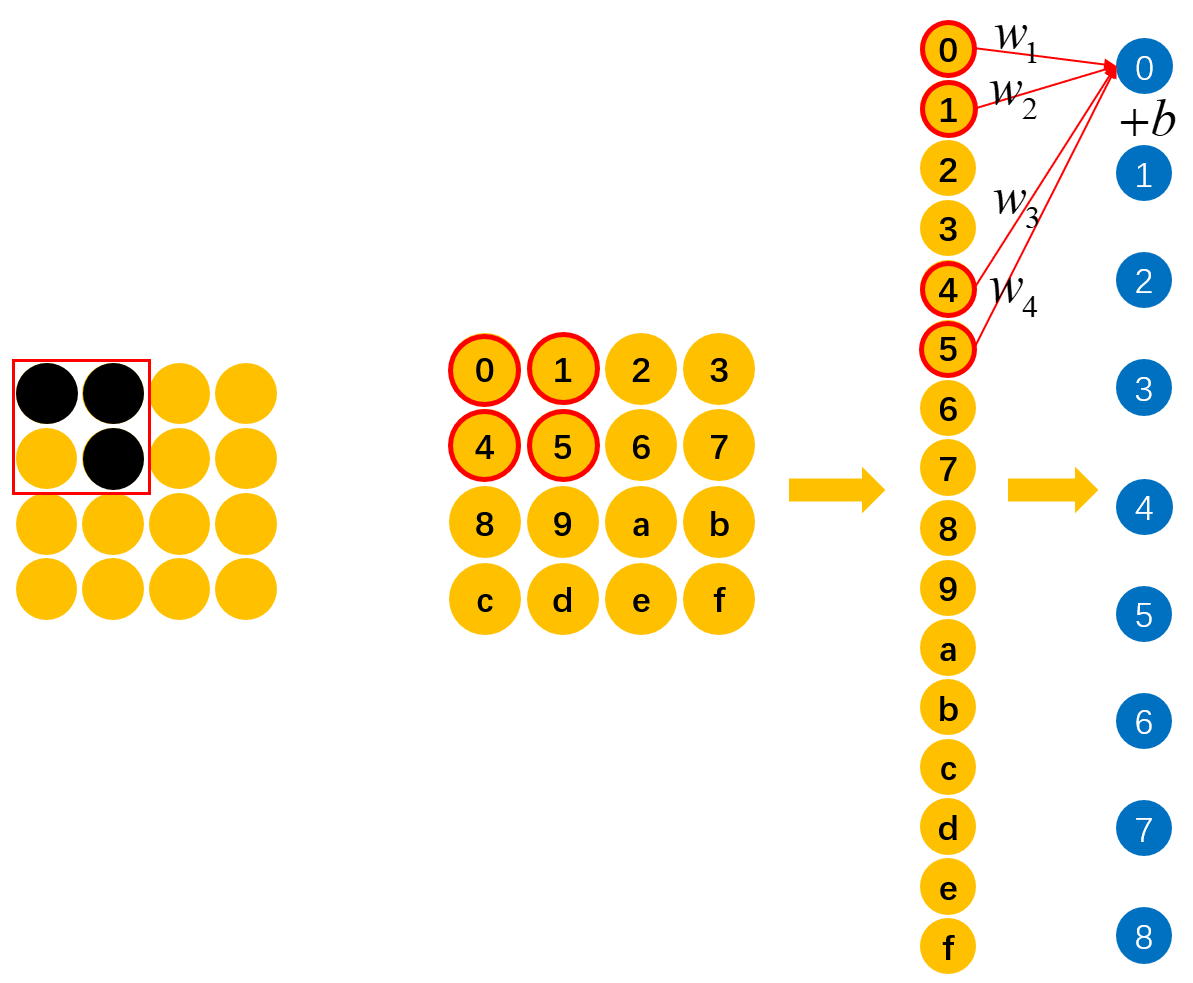
如图13所示，假定一开始“横折”位于最左上角，也就是"0,1,4,5"的位置上，并且此时通过$w_1,w_2,w_3,w_4$能够准确的识别出“0,1,4,5”上是否包含有“横折这么一个元素。那现在问题来了，如果上面的“横折”向右移动了一个格子，那么如何才能快速有效的识别到“横折”这个元素呢？

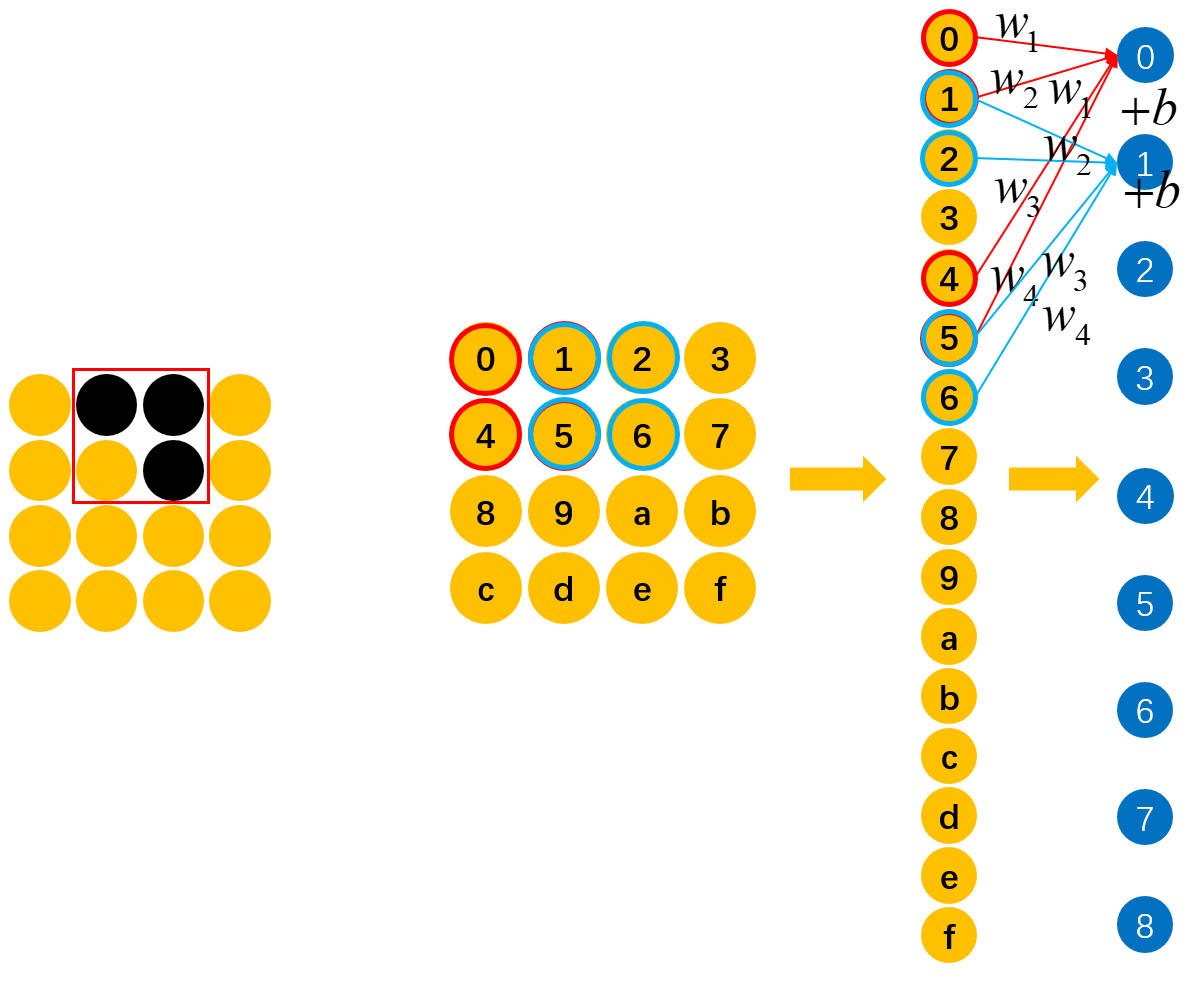
如图14所示，一个有效的快速的识别方法就是，直接同样用$w_1,w_2,w_3,w_4$来对"1,2,5,6"位置上的元素进行识别，判断其是否含有“横折”。有人可能会问，为什么可以这么做呢？原因也很简单，从图13可以看出，$w_1,w_2,w_3,w_4$具有识别“横折”的能力并不是因为权重所在的位置，而是由训练集中“横折”的位置使得对应位置上的权重有了这种能力。既然如此，那我们当然可以将这些具备识别能力权重用于其它位置。换句话说，要是一开始训练数据中的“横折”就位于图14中的位置，那么对应"1,2,5,6"位置上的权重就具备了识别“横折”的能力。

因此，将具有识别某种特征能力的权重共享到其它位置上就是卷积操作的核心思想，它就像一个“扫描器”一样，能够逐个扫描所有位置上是否包含有“扫描器”能够识别的对应元素。

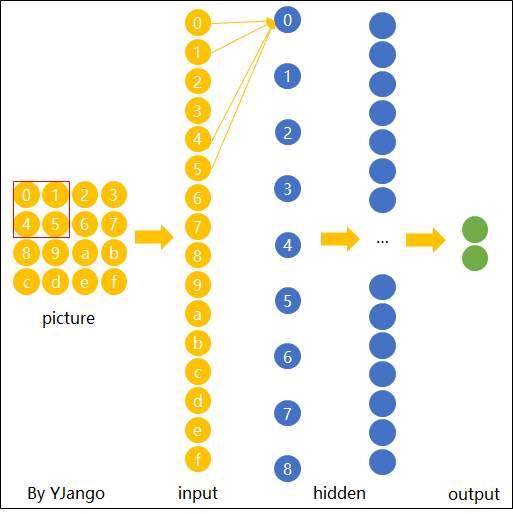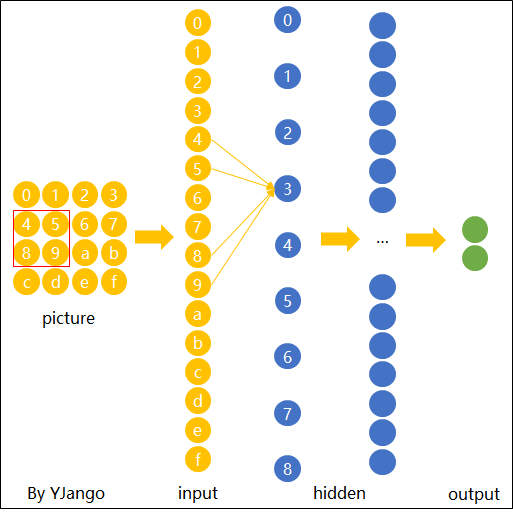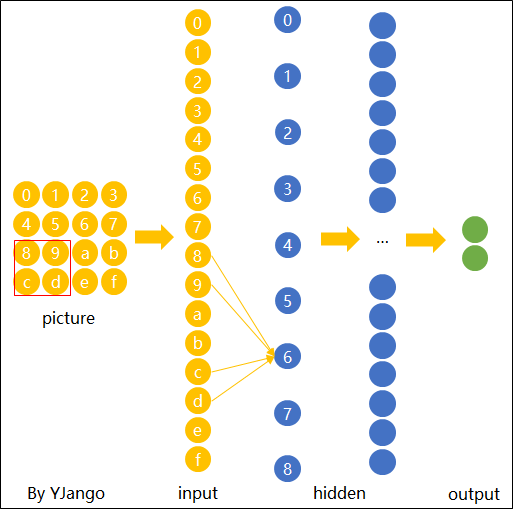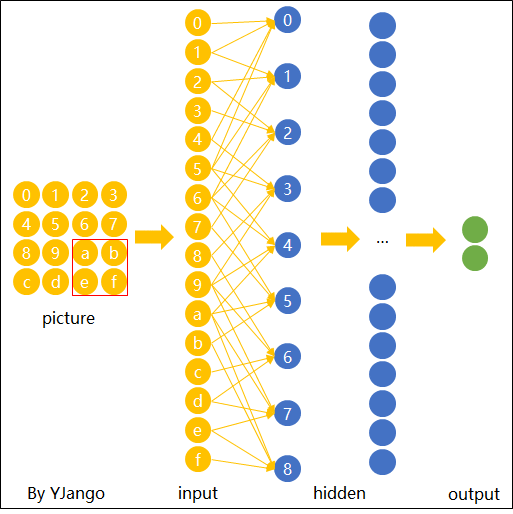
如图15所示，我们在对输入的图片进行特征提取时，不管潜在的“横折”位于什么位置，我只需要用同一组权重对其每个位置进行扫描即可，只要某个位置存在“横折”这么一个元素，那么模型都能将其识别出来。由此我们便可以得出卷积操作的核心原理，那就是在空间上共享权重。可以发现，相较于全连接操作，卷积操作在参数量少有了极剧的减少。到此为止，对于卷积操作的核心原理就介绍完了。在下一篇文章中笔者将会进一步对卷积操作的运算过程、深层卷积以及其中的常见术语进行介绍。

3 总结

在这篇文章中，笔者首先再次抛出了深度学习的理念，即对输入进行深层次的特征提取，然后进行后续的相关任务；接着笔者引出了对于图像处理的相关模型来说，其应该具备的四种基本特性；最后，通过比较全连接操作与卷积操作在对图片进行特征提取时的不同之处，来介绍了卷积操作的工作原理。总结起来就是，所谓卷积其实就是针对于（类）图像数据的一种特征提取方式。

本次内容就到此结束，感谢您的阅读！如果你觉得上述内容对你有所帮助，欢迎关注并传播本公众号！若有任何疑问与建议，请添加笔者微信'nulls8'加群进行交流。青山不改，绿水长流，我们月来客栈见！

引用

[1]卷积：https://baike.baidu.com/item/%E5%8D%B7%E7%A7%AF/9411006?fr=aladdin

[2]图片来源：https://stats.stackexchange.com/questions/208936/what-is-translation-invariance-in-computer-vision-and-convolutional-neural-netwo/208949

[3]YJango的卷积神经网络：https://zhuanlan.zhihu.com/p/27642620

[4]李宏毅https://www.bilibili.com/video/BV1JE411g7XF?p=17

[5]示例代码：https://github.com/moon-hotel/DeepLearningWithMe

推荐阅读

[1]什么你还不会实现反向传播？

[2]l.backward你到底是个什么东西

[3]Pytorch之多层感知机分类任务

[3]我告诉你什么是深度学习